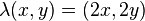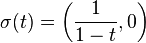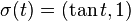Clifton–Pohl torus

From Wikipedia, the free encyclopedia

In geometry, the Clifton–Pohl torus is an example of a compact Lorentzian manifold that is not geodesically complete. While every compact Riemannian manifold is also geodesically complete (by the Hopf–Rinow theorem), this space shows that the same implication does not generalize to pseudo-Riemannian manifolds.^[1] It is named after Yeaton H. Clifton and William F. Pohl, who described it in 1962 but did not publish their result.^[2]

Definition

Consider the manifold 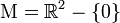${\mathrm {M}}={\mathbb {R}}^{2}-\{0\}$ with the metric

$g={\frac {dx\otimes dy+dy\otimes dx}{x^{2}+y^{2}}}$

Multiplication by any real number is an isometry of $M$ , in particular including the map:

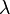$\lambda (x,y)=(2x,2y)$

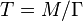Let $\Gamma$ be the subgroup of the isometry group generated by $\lambda$ . Then $\Gamma$ has a proper, discontinuous action on $M$ . Hence the quotient $T=M/\Gamma$ , which is topologically the torus, is a Lorentz surface.^[1]

Geodesic incompleteness

It can be verified that the curve

$\sigma (t)=\left({\frac {1}{1-t}},0\right)$

is a geodesic of M that is not complete (since it is not defined at 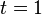$t=1$ ).^[1] Consequently, $M$ (hence also $T$ ) is geodesically incomplete, despite the fact that $T$ is compact. Similarly, the curve

$\sigma (t)=(\tan t,1)$

is a null geodesic that is incomplete. In fact, every null geodesic on $M$ or $T$ is incomplete.

References

↑ 1.0 1.1 1.2 O'Neill, Barrett (1983), Semi-Riemannian Geometry With Applications to Relativity, Pure and Applied Mathematics 103, Academic Press, p. 193, ISBN 9780080570570 .
↑ Wolf, Joseph A. (2011), Spaces of constant curvature (6th ed.), AMS Chelsea Publishing, Providence, RI, p. 95, ISBN 978-0-8218-5282-8, MR 2742530 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.