Circle bundle

From Wikipedia, the free encyclopedia

In mathematics, an (oriented) circle bundle is an oriented fiber bundle where the fiber is the circle $\scriptstyle {\mathbf {S}}^{1}$ , or, more precisely, a principal U(1)-bundle. It is homotopically equivalent to a complex line bundle with removed zero section. In physics, circle bundles are the natural geometric setting for electromagnetism. A circle bundle is a special case of a sphere bundle.

As 3-manifolds

Circle bundles over surfaces are an important example of 3-manifolds. A more general class of 3-manifolds is Seifert fiber spaces, which may be viewed as a kind of "singular" circle bundle, or as a circle bundle over a two-dimensional orbifold.

Relationship to electrodynamics

The Maxwell equations correspond to an electromagnetic field represented by a 2-form F, with $\scriptstyle \pi ^{{\!*}}F$ being cohomologous to zero. In particular, there always exists a 1-form A such that

$\scriptstyle \pi ^{{\!*}}F=dA.$

Given a circle bundle P over M and its projection

$\pi :P\to M$

one has the homomorphism

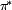$\scriptstyle \pi ^{*}:H^{2}(M,{\mathbb {Z}})\to H^{2}(P,{\mathbb {Z}})$

where $\scriptstyle \pi ^{{\!*}}$ is the pullback. Each homomorphism corresponds to a Dirac monopole; the integer cohomology groups correspond to the quantization of the electric charge.

Examples

The Hopf fibrations are examples of non-trivial circle bundles.

Classification

The isomorphism classes of circle bundles over a manifold M are in one-to-one correspondence with the elements of the second integral cohomology group $\scriptstyle H^{2}(M,{\mathbb {Z}})$ of M. This isomorphism is realized by the Euler class.

Equivalently, the isomorphism classes correspond to homotopy classes of maps to the infinite-dimensional complex projective space 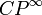$CP^{\infty }$ , which is the classifying space of U(1). See classifying space for U(n).

In homotopy theory terms, the circle and the complex plane without its origin are equivalent. Circle bundles are, by the associated bundle construction, equivalent to smooth complex line bundles because the transition functions of both can be made to live in C*. In this situation, the Euler class of the circle bundle or real two-plane bundle is the same as the first Chern class of the line bundle.

References

Weisstein, Eric W., "Circle Bundle", MathWorld.
Chern, Shiing-shen (1977), "Circle bundles", Lecture Notes in Mathematics, 597/1977, Springer Berlin/Heidelberg, pp. 114–131, ISBN 978-3-540-08345-0 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.