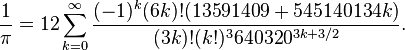Chudnovsky algorithm

From Wikipedia, the free encyclopedia

The Chudnovsky algorithm is a fast method for calculating the digits of π. It was published by the Chudnovsky brothers in 1989,[1] and was used in the world record calculations of 2.7 trillion digits of π in December 2009,[2] 5 trillion digits of π in August 2010,[3] and 10 trillion digits of π in October 2011.[4][5]

The algorithm is based on the following rapidly convergent generalized hypergeometric series:[2]

{\frac {1}{\pi }}=12\sum _{{k=0}}^{\infty }{\frac {(-1)^{k}(6k)!(13591409+545140134k)}{(3k)!(k!)^{3}640320^{{3k+3/2}}}}.\!

This identity is similar to some of Ramanujan's formulas involving π.[2]

See also

  • Numerical approximations of π

References

  1. ↑ Chudnovsky, David V.; Chudnovsky, Gregory V. (1989), "The Computation of Classical Constants", Proceedings of the National Academy of Sciences of the United States of America 86 (21): 8178–8182, doi:10.1073/pnas.86.21.8178, ISSN 0027-8424, JSTOR 34831, PMC 298242, PMID 16594075 .
  2. ↑ 2.0 2.1 2.2 Baruah, Nayandeep Deka; Berndt, Bruce C.; Chan, Heng Huat (2009), "Ramanujan's series for 1/π: a survey", American Mathematical Monthly 116 (7): 567–587, doi:10.4169/193009709X458555, JSTOR 40391165, MR 2549375 .
  3. ↑ Geeks slice pi to 5 trillion decimal places, Australian Broadcasting Corporation, August 6, 2010 .
  4. ↑ Yee, Alexander; Kondo, Shigeru (2011), 10 Trillion Digits of Pi: A Case Study of summing Hypergeometric Series to high precision on Multicore Systems, Technical Report, Computer Science Department, University of Illinois .
  5. ↑ Aron, Jacob (March 14, 2012), "Constants clash on pi day", NewScientist .
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.