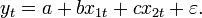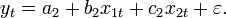Chow test

From Wikipedia, the free encyclopedia

The Chow test is a statistical and econometric test of whether the coefficients in two linear regressions on different data sets are equal. The Chow test was invented by economist Gregory Chow in 1960. In econometrics, the Chow test is most commonly used in time series analysis to test for the presence of a structural break. In program evaluation, the Chow test is often used to determine whether the independent variables have different impacts on different subgroups of the population.

structural break	program evaluation

At $x=1.7$ there is a structural break, regression on the subintervals $[0,1.7]$ and $[1.7,4]$ delivers a better modelling than the combined regression(dashed) over the whole interval.	Comparison of 2 different programs (red, green) existing in a common data set, separate regressions for both programs deliver a better modelling than a combined regression (black).

Suppose that we model our data as

$y_{t}=a+bx_{{1t}}+cx_{{2t}}+\varepsilon .\,$

If we split our data into two groups, then we have

$y_{t}=a_{1}+b_{1}x_{{1t}}+c_{1}x_{{2t}}+\varepsilon .\,$

and

$y_{t}=a_{2}+b_{2}x_{{1t}}+c_{2}x_{{2t}}+\varepsilon .\,$

The null hypothesis of the Chow test asserts that 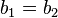$a_{1}=a_{2}$ , $b_{1}=b_{2}$ , and $c_{1}=c_{2}$ , and there is the assumption that the model errors $\varepsilon$ are independent and identically distributed from a normal distribution with unknown variance.

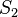Let $S_{C}$ be the sum of squared residuals from the combined data, $S_{1}$ be the sum of squared residuals from the first group, and $S_{2}$ be the sum of squared residuals from the second group. $N_{1}$ and $N_{2}$ are the number of observations in each group and $k$ is the total number of parameters (in this case, 3). Then the Chow test statistic is

${\frac {(S_{C}-(S_{1}+S_{2}))/(k)}{(S_{1}+S_{2})/(N_{1}+N_{2}-2k)}}.$

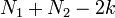The test statistic follows the F distribution with $k$ and $N_{1}+N_{2}-2k$ degrees of freedom.

References

Chow, Gregory C. (1960). "Tests of Equality Between Sets of Coefficients in Two Linear Regressions". Econometrica 28 (3): 591–605. doi:10.2307/1910133. JSTOR 1910133.
Doran, Howard E. (1989). Applied Regression Analysis in Econometrics. CRC Press. p. 146. ISBN 0-8247-8049-3. (restricted online version (Google Books))
Dougherty, Christopher (2007). Introduction to Econometrics. Oxford University Press. p. 194. ISBN 0-19-928096-7. (restricted online version (Google Books))

External links

Computing the Chow statistic, Chow and Wald tests, Chow tests: Series of FAQ explanations from the Stata Corporation at http://www.stata.com/support/faqs/

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.