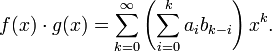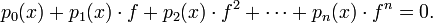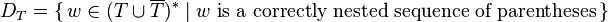Chomsky–Schützenberger theorem
In formal language theory, the Chomsky–Schützenberger theorem is either of two different theorems derived by Noam Chomsky and Marcel-Paul Schützenberger.
One of the two theorems is a statement about the number of words of a given length generated by an unambiguous context-free grammar. The theorem provides an unexpected link between the theory of formal languages and abstract algebra.
The other theorem, which bears the same name (Hotz & Kretschmer 1989), is a statement about representing a given context-free language in terms of two simpler languages. These two simpler languages, namely a regular language and a Dyck language, are combined by means of an intersection and a homomorphism.
Statement of the theorem about counting words
In order to state the theorem, a few notions from algebra and formal language theory are needed.
A power series over  is an infinite series of the form
is an infinite series of the form
with coefficients  in
in  . The multiplication of two formal power series
. The multiplication of two formal power series  and
and 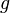 is defined in the expected way as the convolution of the sequences
is defined in the expected way as the convolution of the sequences  and
and 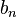 :
:
In particular, we write 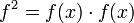 ,
, 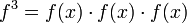 , and so on. In analogy to algebraic numbers, a power series
, and so on. In analogy to algebraic numbers, a power series  is called algebraic over
is called algebraic over 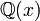 , if there exists a finite set of polynomials
, if there exists a finite set of polynomials 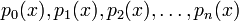 each with rational coefficients such that
each with rational coefficients such that
A context-free grammar is said to be unambiguous if every string generated by the grammar admits a unique parse tree, or, equivalently, only one leftmost derivation. Having established the necessary notions, the theorem is stated as follows.
- Chomsky–Schützenberger theorem. If
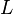 is a context-free language admitting an unambiguous context-free grammar, and
is a context-free language admitting an unambiguous context-free grammar, and  is the number of words of length
is the number of words of length  in
in 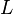 , then
, then 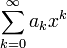 is a power series over
is a power series over  that is algebraic over
that is algebraic over 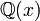 .
.
Proofs of this theorem are given by Kuich & Salomaa (1985), and by Panholzer (2005).
Statement of the theorem about representing context-free languages
Also for the other theorem bearing this name, a few notions from formal language theory are in order. A context-free language is regular, if can be described by a regular expression, or, equivalently, if it is accepted by a finite automaton. A homomorphism is based on a function  which maps symbols from an alphabet
which maps symbols from an alphabet  to words over another alphabet
to words over another alphabet  ; If the domain of this function is extended to words over
; If the domain of this function is extended to words over  in the natural way, by letting
in the natural way, by letting 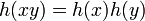 for all words
for all words  and
and  , this yields a homomorphism
, this yields a homomorphism 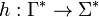 . A matched alphabet
. A matched alphabet  is an alphabet with two equal-sized sets; it is convenient to think of it as a set of parentheses types, where
is an alphabet with two equal-sized sets; it is convenient to think of it as a set of parentheses types, where  contains the opening parenthesis symbols, whereas the symbols in
contains the opening parenthesis symbols, whereas the symbols in 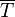 contains the closing parenthesis symbols. For a matched alphabet
contains the closing parenthesis symbols. For a matched alphabet  , the Dyck language
, the Dyck language 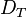 is given by
is given by
words that are well-nested parentheses over  .
.
- Chomsky–Schützenberger theorem. A language L over the alphabet
 is context-free if and only if there exists
is context-free if and only if there exists
- a matched alphabet

- a regular language
 over
over  ,
, - and a homomorphism
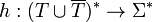
- a matched alphabet
- such that
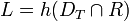 .
.
Proofs of this theorem are given by Hotz & Kretschmer (1989) and Autebert, Berstel & Boasson (1997).
Bibliography
- Autebert, Jean-Michel; Berstel, Jean; Boasson, Luc (1997). "Context-Free Languages and Push-Down Automata". In G. Rozenberg and A. Salomaa, eds., Handbook of Formal Languages, Vol. 1: Word, Language, Grammar (pp. 111–174). Berlin: Springer-Verlag. ISBN 3-540-60420-0.
- Chomsky, Noam; Schützenberger, Marcel-Paul (1963). "The Algebraic Theory of Context-Free Languages". In P. Braffort and D. Hirschberg, eds., Computer Programming and Formal Systems (pp. 118–161). Amsterdam: North-Holland.
- Flajolet, Philippe; Sedgewick, Robert (2009). Analytic Combinatorics. Cambridge: Cambridge University Press. ISBN 978-0-521-89806-5.
- Hotz, G.; Kretschmer, T. (1989). "The power of the Greibach normal form". Elektronische Informationsverarbeitung und Kybernetik 25 (10): 507–512.
- Kuich, Werner; Salomaa, Arto (1985). Semirings, Automata, Languages. Berlin: Springer-Verlag. ISBN 978-3-642-69961-0.
- Panholzer, Alois (2005). "Gröbner Bases and the Defining Polynomial of a Context-free Grammar Generating Function". Journal of Automata, Languages and Combinatorics 10: 79–97.