Chiral superfield

From Wikipedia, the free encyclopedia

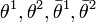In theoretical physics, one often analyzes theories with supersymmetry in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace. Superspace contains the usual space-time coordinates $x^{{\mu }}$ , $\mu =0,\ldots ,3$ , and four extra fermionic coordinates $\theta ^{1},\theta ^{2},{\bar \theta }^{1},{\bar \theta }^{2}$ , transforming as a two-component (Weyl) spinor and its conjugate.

In N=1 supersymmetry in 3+1D, a chiral superfield is a function over chiral superspace. There exists a projection from the (full) superspace to chiral superspace. So, a function over chiral superspace can be pulled back to the full superspace. Such a function satisfies the covariant constraint $\overline {D}f=0$ . Similarly, we also have an antichiral superspace which is the complex conjugate of chiral superspace and antichiral superfields.

Superspace is the homogeneous space of the SUSY supergroup with the Lorentz group as the stabilizer. Chiral superspace is the homogeneous space with the supergroup generated by the Lorentz transformations and 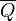$\overline {Q}$ as the stabilizer. Clearly, there is a projection from the former to the latter.

Every superfield—i.e. a field that depends on all coordinates of the superspace—may be expanded with respect to the fermionic coordinates. There exists a special kind of superfields, the so-called chiral superfields, that, in the chiral representation of supersymmetry, depend only on the variables 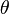$\theta$ but not their conjugates. See also F-terms.

Chiral superfields satisfy the relation 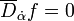$\overline {D}_{{{\dot {\alpha }}}}f=0$ . They can also be expressed as fields over chiral superspace.