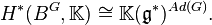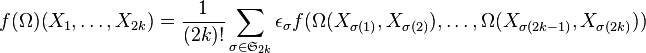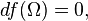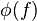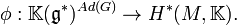Chern–Weil homomorphism

From Wikipedia, the free encyclopedia

In mathematics, the Chern–Weil homomorphism is a basic construction in the Chern–Weil theory, relating for a smooth manifold M the curvature of M to the de Rham cohomology groups of M, i.e., geometry to topology. This theory of Shiing-Shen Chern and André Weil from the 1940s was an important step in the theory of characteristic classes. It is a generalization of the Chern–Gauss–Bonnet theorem.

Denote by ${\mathbb K}$ either the real field or complex field. Let G be a real or complex Lie group with Lie algebra ${\mathfrak g}$ ; and let

${\mathbb K}({\mathfrak g}^{*})$

denote the algebra of ${\mathbb K}$ -valued polynomials on ${\mathfrak g}$ . Let ${\mathbb K}({\mathfrak g}^{*})^{{Ad(G)}}$ be the subalgebra of fixed points in ${\mathbb K}({\mathfrak g}^{*})$ under the adjoint action of G, so that for instance

$f(t_{1},\dots ,t_{k})=f(Ad_{g}t_{1},\dots ,Ad_{g}t_{k})\,$

for all $f\in {\mathbb K}({\mathfrak g}^{*})^{{Ad(G)}}.\,$

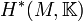The Chern–Weil homomorphism is a homomorphism of ${\mathbb K}$ -algebras from ${\mathbb K}({\mathfrak g}^{*})^{{Ad(G)}}$ to the cohomology algebra $H^{*}(M,{\mathbb K})$ . Such a homomorphism exists and is uniquely defined for every principal G-bundle P on M. If G is compact, then under the homomorphism, the cohomology ring of the classifying space for G-bundles B^G is isomorphic to the algebra ${\mathbb K}({\mathfrak g}^{*})^{{Ad(G)}}$ of invariant polynomials:

$H^{*}(B^{G},{\mathbb {K}})\cong {\mathbb K}({\mathfrak g}^{*})^{{Ad(G)}}.$

For non-compact groups like SL(n,R), there may be cohomology classes that are not represented by invariant polynomials.

Definition of the homomorphism

Choose any connection form w in P, and let $\Omega$ be the associated curvature 2-form. If $f\in {\mathbb K}({\mathfrak g}^{*})^{{Ad(G)}}$ is a homogeneous polynomial of degree k, let $f(\Omega )$ be the 2k-form on P given by

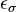$f(\Omega )(X_{1},\dots ,X_{{2k}})={\frac {1}{(2k)!}}\sum _{{\sigma \in {\mathfrak S}_{{2k}}}}\epsilon _{\sigma }f(\Omega (X_{{\sigma (1)}},X_{{\sigma (2)}}),\dots ,\Omega (X_{{\sigma (2k-1)}},X_{{\sigma (2k)}}))$

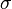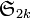where $\epsilon _{\sigma }$ is the sign of the permutation $\sigma$ in the symmetric group on 2k numbers ${\mathfrak S}_{{2k}}$ .

(see Pfaffian).

One can then show that

$f(\Omega )$

is a closed form, so that

$df(\Omega )=0,\,$

and that the de Rham cohomology class of

$f(\Omega )\,$

is independent of the choice of connection on P, so it depends only upon the principal bundle.

Thus letting

$\phi (f)\,$

be the cohomology class obtained in this way from f, we obtain an algebra homomorphism

$\phi :{\mathbb K}({\mathfrak g}^{*})^{{Ad(G)}}\rightarrow H^{*}(M,{\mathbb K}).\,$

References

Bott, R. (1973), "On the Chern–Weil homomorphism and the continuous cohomology of Lie groups", Advances in Math 11: 289–303, doi:10.1016/0001-8708(73)90012-1 .
Chern, S.-S. (1951), Topics in Differential Geometry, Institute for Advanced Study, mimeographed lecture notes .
Shiing-Shen Chern, Complex Manifolds Without Potential Theory (Springer-Verlag Press, 1995) ISBN 0-387-90422-0, ISBN 3-540-90422-0.
The appendix of this book: "Geometry of Characteristic Classes" is a very neat and profound introduction to the development of the ideas of characteristic classes.
Chern, S.-S.; Simons, J (1974), "Characteristic forms and geometric invariants", The Annals of Mathematics. Second Series 99 (1): 48–69, JSTOR 1971013 .
Kobayashi, S.; Nomizu, K. (1963), Foundations of Differential Geometry, Vol. 2, Wiley-Interscience (published new ed. 2004) .
Narasimhan, M.; Ramanan, S. (1961), "Existence of universal connections", Amer. J. Math. 83: 563–572, doi:10.2307/2372896, JSTOR 2372896 .
Morita, Shigeyuki (2000), "Geometry of Differential Forms", A.M.S monograph 201 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.