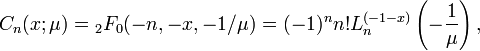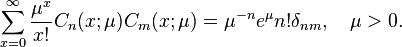Charlier polynomials

From Wikipedia, the free encyclopedia

In mathematics, Charlier polynomials (also called Poisson–Charlier polynomials) are a family of orthogonal polynomials introduced by Carl Charlier. They are given in terms of the generalized hypergeometric function by

$C_{n}(x;\mu )={}_{2}F_{0}(-n,-x,-1/\mu )=(-1)^{n}n!L_{n}^{{(-1-x)}}\left(-{\frac 1\mu }\right),\,$

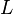where $L$ are Laguerre polynomials. They satisfy the orthogonality relation

$\sum _{{x=0}}^{\infty }{\frac {\mu ^{x}}{x!}}C_{n}(x;\mu )C_{m}(x;\mu )=\mu ^{{-n}}e^{\mu }n!\delta _{{nm}},\quad \mu >0.$

References

C. V. L. Charlier (1905–1906) Über die Darstellung willkürlicher Funktionen, Ark. Mat. Astr. och Fysic 2, 20.
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), "Hahn Class: Definitions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
Szegő, Gabor (1939), Orthogonal Polynomials, Colloquium Publications – American Mathematical Society, ISBN 978-0-8218-1023-1, MR 0372517

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.