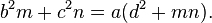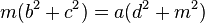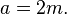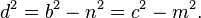Cevian
From Wikipedia, the free encyclopedia
In geometry, a cevian is any line segment in a triangle with one endpoint on a vertex of the triangle and the other endpoint on the opposite side. Medians, altitudes, and angle bisectors are special cases of cevians. The name cevian comes from the Italian engineer Giovanni Ceva, who proved a well known theorem about cevians which also bears his name.
Length

A triangle with a cevian
The length of a cevian can be determined by Stewart's Theorem. In the diagram, the length  can be determined from the formula
can be determined from the formula
If the cevian happens to be a median, its length can be determined from the formula
or
as
If the cevian happens to be an angle bisector, its length can be determined from the formula
If the cevian happens to be an altitude, its length can be determined from the formula
See also
References
- Ross Honsberger (1995) Episodes in Nineteenth and Twentieth Century Euclidean Geometry, pages 13 and 137, Mathematical Association of America.
- Vladimir Karapetoff (1929) "Some properties of correlative vertex lines in a plane triangle", American Mathematical Monthly 36:476–9.
- Indika Shameera Amarasinghe (2011) A New Theorem on any Right-angled Cevian Triangle, Journal of the World Federation of National Mathematics Competitions, Vol 24(02), pp.29 - 37.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.