Centripetal Catmull–Rom spline

From Wikipedia, the free encyclopedia

Used in mathematics and computer graphics, the centripetal Catmull–Rom spline is a curve named after Edwin Catmull and Raphael Rom. The principle advantage of this technique is that the original set of points also make up the control points for the spline curve.[1] Two additional points are required on either end of the curve. The default implementation of the Catmull–Rom algorithm is capable of producing loops and self intersections. The chordal and centripetal Catmull–Rom implementations [2] were introduced as a solution to this problem using a slightly different calculation.[3] It has been shown that only the centripetal parameterization will not form cusps or self-intersections.[4] In computer graphics, Catmull–Rom splines are frequently used to get smooth interpolated motion between key frames. For example, most camera path animations generated from discrete key-frames are handled using Catmull–Rom splines. They are popular mainly for being relatively easy to compute, guaranteeing that each key frame position will be hit exactly, and also guaranteeing that the tangents of the generated curve are continuous over multiple segments.

Definition

The centripetal Catmull–Rom is a subclass of cubic Hermite spline that extends the Catmull–Rom implementation by allowing each of the four control points to be associated with an arbitrary time interval in the computation of a value on the curve. This modifies the behavior of the curve. The curve is an interpolation, and will intersect with all but the first and last control points. If the time intervals are uniform, the result will be the same as that of the original Catmull–Rom spline curve. The chordal curve uses the two dimensional Euclidean distance between control points to provide the time elements, while the centripetal curve uses the square root of the Euclidean distance. The principle reason for using the centripetal version is that it has been shown to be free of cusps and self-intersections.[5] http://www.cemyuksel.com/research/catmullrom_param/catmullrom.pdf

Methodology

Catmull–Rom spline interpolation with four points

Like the standard Catmull–Rom calculation, the curve formulation requires the use of four points at a time, creating an interpolation between P1 and P2, and uses P0 and P3 as control points. The X and Y values are computed independently. An X or Y value on the curve at time t can be computed using the Barry and Goldman's pyramidal formulation, which is illustrated in the figure to the right.

Barry and Goldman's pyramidal formulation

The benefit of using Barry and Goldman's formulation in the pyramid diagram is that it allows for the calculation to take place with arbitrary time spacing. The diagram should be interpreted as multiplying the original control point values (P0 − P3) by the ratios along the arrows, and adding the products together to get the values on the next level. This is then repeated for the levels shown as B and C in the diagram. The value at C will be the final X or Y value at time t along the interpolated curve. The time axis is different from the un-parameterized Catmull–Rom algorithm because in the original Catmull–Rom calculation, time is measured from 0 to 1 between P1 and P2 with no contribution from outside the interpolated segment, and no ability to pass in time values. In the time parameterized version, time starts at 0 with P0 and increased continuously to P3. In the uniform case, the time values are chosen in equal portions, i.e. 0, 1, 2 and 3. So in order to calculate points on the curve between P1 and P2, t values between 1 and 2 would be used.

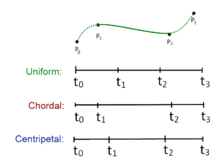
Time parameterization for the Catmull–Rom algorithm.

The time axis is shown in the figure for the different relative lengths of time. In the Chordal case, each time interval is proportional to the Euclidean distance between the two points. In the Centripetal case, each time interval is the square root of the Euclidean distance between the points. The impact on the "stiffness" of the curve can be seen in the example curves shown below.

See also

Cubic Hermite splines

Implementation in Java

References

  1. ↑ E. Catmull and R. Rom. A class of local interpolating splines. Computer Aided Geometric Design, pages 317-326, 1974.
  2. ↑ N. Dyn, M. S. Floater, and K. Hormann. Four-point curve subdivision based on iterated chordal and centripetal parameterizations. Computer Aided Geometric Design, 26(3):279-286, 2009
  3. ↑ P. J. Barry and R. N. Goldman. A recursive evaluation algorithm for a class of Catmull–Rom splines. SIGGRAPH Computer Graphics, 22(4):199{204, 1988.
  4. ↑ C. Yuksel, S. Schaefer, J. Keyser. On the Parameterization of Catmull–Rom Curves. Proceeding SPM '09 2009 SIAM/ACM Joint Conference on Geometric and Physical Modeling. Pages 47–53. ACM New York, NY, USA ISBN 978-1-60558-711-0 doi>10.1145/1629255.1629262
  5. ↑ C. Yuksel, S. Schaefer, J. Keyser. On the Parameterization of Catmull–Rom Curves. Proceeding SPM '09 2009 SIAM/ACM Joint Conference on Geometric and Physical Modeling. Pages 47–53. ACM New York, NY, USA ©2009 table of contents ISBN 978-1-60558-711-0 doi>10.1145/1629255.1629262
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.