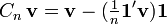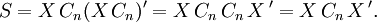Centering matrix
In mathematics and multivariate statistics, the centering matrix[1] is a symmetric and idempotent matrix, which when multiplied with a vector has the same effect as subtracting the mean of the components of the vector from every component.
Definition
The centering matrix of size n is defined as the n-by-n matrix
where  is the identity matrix of size n and
is the identity matrix of size n and 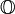 is an n-by-n matrix of all 1's. This can also be written as:
is an n-by-n matrix of all 1's. This can also be written as:
where  is the column-vector of n ones and where
is the column-vector of n ones and where  denotes matrix transpose.
denotes matrix transpose.
For example
 ,
,
![C_{2}=\left[{\begin{array}{rrr}1&0\\\\0&1\end{array}}\right]-{\frac {1}{2}}\left[{\begin{array}{rrr}1&1\\\\1&1\end{array}}\right]=\left[{\begin{array}{rrr}{\frac {1}{2}}&-{\frac {1}{2}}\\\\-{\frac {1}{2}}&{\frac {1}{2}}\end{array}}\right]](/2014-wikipedia_en_all_02_2014/I/media/6/a/a/d/6aad4056a10bf0626f63eaeda55d4407.png) ,
,
Properties
Given a column-vector, 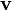 of size n, the centering property of
of size n, the centering property of 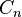 can be expressed as
can be expressed as
where 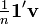 is the mean of the components of
is the mean of the components of 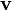 .
.
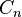 is symmetric positive semi-definite.
is symmetric positive semi-definite.
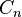 is idempotent, so that
is idempotent, so that 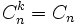 , for
, for 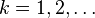 . Once the mean has been removed, it is zero and removing it again has no effect.
. Once the mean has been removed, it is zero and removing it again has no effect.
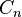 is singular. The effects of applying the transformation
is singular. The effects of applying the transformation 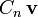 cannot be reversed.
cannot be reversed.
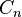 has the eigenvalue 1 of multiplicity n − 1 and eigenvalue 0 of multiplicity 1.
has the eigenvalue 1 of multiplicity n − 1 and eigenvalue 0 of multiplicity 1.
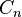 has a nullspace of dimension 1, along the vector
has a nullspace of dimension 1, along the vector  .
.
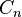 is a projection matrix. That is,
is a projection matrix. That is,  is a projection of
is a projection of 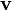 onto the (n − 1)-dimensional subspace that is orthogonal to the nullspace
onto the (n − 1)-dimensional subspace that is orthogonal to the nullspace  . (This is the subspace of all n-vectors whose components sum to zero.)
. (This is the subspace of all n-vectors whose components sum to zero.)
Application
Although multiplication by the centering matrix is not a computationally efficient way of removing the mean from a vector, it forms an analytical tool that conveniently and succinctly expresses mean removal. It can be used not only to remove the mean of a single vector, but also of multiple vectors stored in the rows or columns of a matrix. For an m-by-n matrix 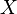 , the multiplication
, the multiplication 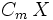 removes the means from each of the n columns, while
removes the means from each of the n columns, while 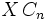 removes the means from each of the m rows.
removes the means from each of the m rows.
The centering matrix provides in particular a succinct way to express the scatter matrix, 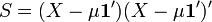 of a data sample
of a data sample 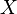 , where
, where  is the sample mean. The centering matrix allows us to express the scatter matrix more compactly as
is the sample mean. The centering matrix allows us to express the scatter matrix more compactly as
 is the covariance matrix of the multinomial distribution, in the special case where the parameters of that distribution are
is the covariance matrix of the multinomial distribution, in the special case where the parameters of that distribution are 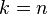 , and
, and  .
.
References
- ↑ John I. Marden, Analyzing and Modeling Rank Data, Chapman & Hall, 1995, ISBN 0-412-99521-2, page 59.
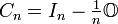
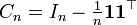
![C_{3}=\left[{\begin{array}{rrr}1&0&0\\\\0&1&0\\\\0&0&1\end{array}}\right]-{\frac {1}{3}}\left[{\begin{array}{rrr}1&1&1\\\\1&1&1\\\\1&1&1\end{array}}\right]=\left[{\begin{array}{rrr}{\frac {2}{3}}&-{\frac {1}{3}}&-{\frac {1}{3}}\\\\-{\frac {1}{3}}&{\frac {2}{3}}&-{\frac {1}{3}}\\\\-{\frac {1}{3}}&-{\frac {1}{3}}&{\frac {2}{3}}\end{array}}\right]](/2014-wikipedia_en_all_02_2014/I/media/f/8/6/d/f86d231d8fd48f68f3359346200bab52.png)