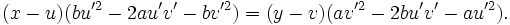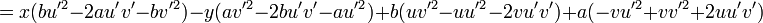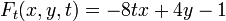Caustic (mathematics)

From Wikipedia, the free encyclopedia

In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the concept of caustics in optics. The ray's source may be a point (called the radiant) or parallel rays from a point at infinity, in which case a direction vector of the rays must be specified.

More generally, especially as applied to symplectic geometry and singularity theory, a caustic is the critical value set of a Lagrangian mapping (π ○ i) : L ↪ M ↠ B; where i : L ↪ M is a Lagrangian immersion of a Lagrangian submanifold L into a symplectic manifold M, and π : M ↠ B is a Lagrangian fibration of the symplectic manifold M. The caustic is a subset of the Lagrangian fibration's base space B.[1]

Catacaustic

A catacaustic is the reflective case.

With a radiant, it is the evolute of the orthotomic of the radiant.

The planar, parallel-source-rays case: suppose the direction vector is (a,b) and the mirror curve is parametrised as 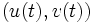(u(t),v(t)). The normal vector at a point is (-v'(t),u'(t)); the reflection of the direction vector is (normal needs special normalization)

2{\mbox{proj}}_{n}d-d={\frac {2n}{{\sqrt {n\cdot n}}}}{\frac {n\cdot d}{{\sqrt {n\cdot n}}}}-d=2n{\frac {n\cdot d}{n\cdot n}}-d={\frac {(av'^{2}-2bu'v'-au'^{2},bu'^{2}-2au'v'-bv'^{2})}{v'^{2}+u'^{2}}}

Having components of found reflected vector treat it as a tangent

(x-u)(bu'^{2}-2au'v'-bv'^{2})=(y-v)(av'^{2}-2bu'v'-au'^{2}).

Using the simplest envelope form

F(x,y,t)=(x-u)(bu'^{2}-2au'v'-bv'^{2})-(y-v)(av'^{2}-2bu'v'-au'^{2}) =x(bu'^{2}-2au'v'-bv'^{2})-y(av'^{2}-2bu'v'-au'^{2})+b(uv'^{2}-uu'^{2}-2vu'v')+a(-vu'^{2}+vv'^{2}+2uu'v')
F_{t}(x,y,t)=2x(bu'u''-a(u'v''+u''v')-bv'v'')-2y(av'v''-b(u''v'+u'v'')-au'u'')+b(u'v'^{2}+2uv'v''-u'^{3}-2uu'u''-2u'v'^{2}-2u''vv'-2u'vv'')+a(-v'u'^{2}-2vu'u''+v'^{3}+2vv'v''+2v'u'^{2}+2v''uu'+2v'uu'')

which may be unaesthetic, but F=F_{t}=0 gives a linear system in (x,y) and so it is elementary to obtain a parametrisation of the catacaustic. Cramer's rule would serve.

Example

Let the direction vector be (0,1) and the mirror be (t,t^{2}). Then

u'=1   u''=0   v'=2t   v''=2   a=0   b=1
F(x,y,t)=(x-t)(1-4t^{2})+4t(y-t^{2})=x(1-4t^{2})+4ty-t
F_{t}(x,y,t)=-8tx+4y-1

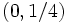and F=F_{t}=0 has solution (0,1/4); i.e., light entering a parabolic mirror parallel to its axis is reflected through the focus.

References

  1. ↑ Arnold, V. I.; Varchenko, A. N.; Gusein-Zade, S. M. (1985). The Classification of Critical Points, Caustics and Wave Fronts: Singularities of Differentiable Maps, Vol 1. Birkhäuser. ISBN 0-8176-3187-9. 

See also

External links

Differential transforms of plane curves
Unary operations
Unary operations defined by a point
Unary operations defined by two points
Binary operations defined by a point
Operations on a family of curves
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.