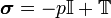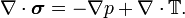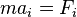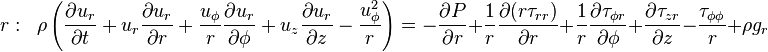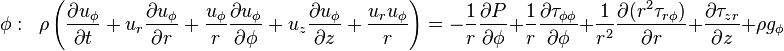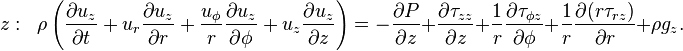Cauchy momentum equation
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum:[1]
or, with the material derivative expanded out,
where  is the density of the continuum,
is the density of the continuum, 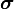 is the stress tensor, and
is the stress tensor, and  contains all of the body forces per unit volume (often simply density times gravity).
contains all of the body forces per unit volume (often simply density times gravity).  is the velocity vector field, which depends on time and space.
is the velocity vector field, which depends on time and space.
The stress tensor is sometimes split into pressure and the deviatoric stress tensor:
where  is the
is the 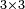 identity matrix and
identity matrix and  the deviatoric stress tensor. The divergence of the stress tensor can be written as
the deviatoric stress tensor. The divergence of the stress tensor can be written as
All non-relativistic momentum conservation equations, such as the Navier–Stokes equation, can be derived by beginning with the Cauchy momentum equation and specifying the stress tensor through a constitutive relation.
Derivation
Applying Newton's second law (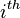 component) to a control volume in the continuum being modeled gives:
component) to a control volume in the continuum being modeled gives:
where  represents the control volume. Since this equation must hold for any control volume, it must be true that the integrand is zero, from this the Cauchy momentum equation follows. The main challenge in deriving this equation is establishing that the derivative of the stress tensor is one of the forces that constitutes
represents the control volume. Since this equation must hold for any control volume, it must be true that the integrand is zero, from this the Cauchy momentum equation follows. The main challenge in deriving this equation is establishing that the derivative of the stress tensor is one of the forces that constitutes  .
.
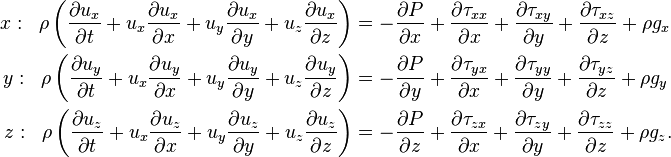
Cartesian coordinates
Cylindrical coordinates
By expressing the shear stress in terms of viscosity and fluid velocity, and assuming constant density and viscosity, the Cauchy momentum equation will lead to the Navier–Stokes equations. By assuming inviscid flow, the Navier–Stokes equations can further simpify to the Euler equations.
See also
References
- ↑ Acheson, D. J. (1990). Elementary Fluid Dynamics. Oxford University Press. p. 205. ISBN 0-19-859679-0.

![\rho \left[{\frac {\partial {\mathbf {v}}}{\partial t}}+({\mathbf {v}}\cdot \nabla ){\mathbf {v}}\right]=\nabla \cdot {\boldsymbol {\sigma }}+{\mathbf {f}}](/2014-wikipedia_en_all_02_2014/I/media/b/d/c/7/bdc779791085f585916bf9380eff384e.png)