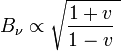Cauchy horizon
In physics, a Cauchy horizon is a light-like boundary of the domain of validity of a Cauchy problem (a particular boundary value problem of the theory of partial differential equations). One side of the horizon contains closed space-like geodesics and the other side contains closed time-like geodesics.
Waves traveling in Misner space approaching a Cauchy horizon would receive a frequency boost proportional to
each time they pass through the identification world line. As this happens infinitely many times while approaching the horizon, the stress-energy tensor diverges at the horizon. Presumably, this prevents spacetime from developing closed time-like curves that would otherwise be feasible.
Under the averaged weak energy condition (AWEC), Cauchy horizons are inherently unstable. However, cases of AWEC violation, such as the Casimir effect, do exist. If we can assume that the spacetime inside the Cauchy horizon violates AWEC, then the horizon becomes stable and frequency boosting effects would be canceled out by the tendency of the spacetime to act as a divergent lens. Were this conjecture to be shown empirically true, it would provide a counter-example to the strong cosmic censorship conjecture.
The simplest example is the internal horizon of a Reissner-Nordström black hole.