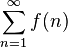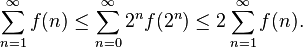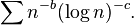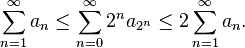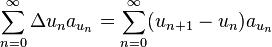Cauchy condensation test

From Wikipedia, the free encyclopedia

Not to be confused with Cauchy's convergence test.

Calculus
Fundamental theorem Limits of functions Continuity Mean value theorem Rolle's theorem
Differential calculus Definitions Derivative Differential (infinitesimal) Differential of a function Generalizations of the derivative Concepts Notation for differentiation Second derivative Third derivative Change of variables Implicit differentiation Related rates Taylor's theorem Rules and identities Sums Products Chain rule Powers Quotients Faà di Bruno's formula
Integral calculus Lists of integrals Definitions Antiderivative Integral Improper integral Riemann integral Lebesgue integration Contour integral Integration by parts discs cylindrical shells substitution trigonometric substitution partial fractions changing order reduction formulae
Series Geometric Arithmetico-geometric Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (Term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector calculus Gradient Divergence Curl Laplacian Gradient theorem Green's theorem Stokes' theorem Divergence theorem Directional derivative
Multivariable calculus Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian
Specialized calculi Calculus of variations Fractional Malliavin Stochastic
v t e

In mathematics, the Cauchy condensation test, named after Augustin-Louis Cauchy, is a standard convergence test for infinite series. For a positive non-increasing sequence f(n), the sum

$\sum _{{n=1}}^{{\infty }}f(n)$

converges if and only if the sum

$\sum _{{n=0}}^{{\infty }}2^{{n}}f(2^{{n}})$

converges. Moreover, in that case we have

$\sum _{{n=1}}^{{\infty }}f(n)\leq \sum _{{n=0}}^{{\infty }}2^{{n}}f(2^{{n}})\leq 2\sum _{{n=1}}^{{\infty }}f(n).$

A geometric view is that we are approximating the sum with trapezoids at every $2^{{n}}$ . Another explanation is that, as with the analogy between finite sums and integrals, the 'condensation' of terms is analogous to a substitution of an exponential function. This becomes clearer in examples such as

$\ f(n)=n^{{-a}}(\log n)^{{-b}}(\log \log n)^{{-c}}.$

Here the series definitely converges for a > 1, and diverges for a < 1. When a = 1, the condensation transformation essentially gives the series

$\sum n^{{-b}}(\log n)^{{-c}}.$

The logarithms 'shift to the left'. So when a = 1, we have convergence for b > 1, divergence for b < 1. When b = 1 the value of c enters.

Proof

Let f(n) be a positive, non-increasing sequence of real numbers. To simplify the notation, we will write a_n = f(n). We are to investigate the series 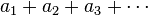$a_{1}+a_{2}+a_{3}+\cdots$ . The condensation test follows from noting that if we collect the terms of the series into groups of lengths $2^{{n}}$ , each of these groups will be less than $2^{{n}}a_{{2^{{n}}}}$ by monotonicity. Observe,

${\begin{aligned}\sum _{{n=1}}^{{\infty }}a_{n}&=a_{1}+\underbrace {a_{2}+a_{3}}_{{\leq a_{2}+a_{2}}}+\underbrace {a_{4}+a_{5}+a_{6}+a_{7}}_{{\leq a_{4}+a_{4}+a_{4}+a_{4}}}+\cdots +\underbrace {a_{{2^{n}}}+a_{{2^{n}+1}}+\cdots +a_{{2^{{n+1}}-1}}}_{{\leq a_{{2^{n}}}+a_{{2^{n}}}+\cdots +a_{{2^{n}}}}}+\cdots \\&\leq a_{1}+2a_{2}+4a_{4}+\cdots +2^{n}a_{{2^{n}}}+\cdots =\sum _{{n=0}}^{{\infty }}2^{n}a_{{2^{n}}}.\end{aligned}}$

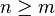We have used the fact that the sequence a_n is non-increasing, thus $a_{n}\leq a_{m}$ whenever $n\geq m$ . The convergence of the original series now follows from direct comparison to this "condensed" series. To see that convergence of the original series implies the convergence of this last series, we similarly put,

${\begin{aligned}\sum _{{n=0}}^{{\infty }}2^{n}a_{{2^{n}}}&=\underbrace {a_{1}+a_{2}}_{{\leq a_{1}+a_{1}}}+\underbrace {a_{2}+a_{4}+a_{4}+a_{4}}_{{\leq a_{2}+a_{2}+a_{3}+a_{3}}}+\cdots +\underbrace {a_{{2^{n}}}+a_{{2^{{n+1}}}}+\cdots +a_{{2^{{n+1}}}}}_{{\leq a_{{2^{n}}}+a_{{2^{n}}}+a_{{(2^{n}+1)}}+a_{{(2^{n}+1)}}+\cdots +a_{{(2^{{n+1}}-1)}}}}+\cdots \\&\leq a_{1}+a_{1}+a_{2}+a_{2}+a_{3}+a_{3}+\cdots +a_{n}+a_{n}+\cdots =2\sum _{{n=1}}^{{\infty }}a_{n}.\end{aligned}}$

And we have convergence, again by direct comparison. And we are done. Note that we have obtained the estimate

$\sum _{{n=1}}^{{\infty }}a_{n}\leq \sum _{{n=0}}^{{\infty }}2^{n}a_{{2^{n}}}\leq 2\sum _{{n=1}}^{{\infty }}a_{n}.$

This proof is a generalization of Oresme's proof of the divergence of the harmonic series.

Generalizations

The following generalization is due to Schlömilch. Let 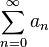$\sum _{{n=0}}^{{\infty }}a_{n}$ be an infinite real series whose terms are positive and non-increasing, and let $u_{0}<u_{1}<u_{2}<\cdots$ be a strictly increasing sequence of positive integers such that

${\frac {\Delta u_{n}}{\Delta u_{{n-1}}}}={\frac {u_{{n+1}}-u_{n}}{u_{n}-u_{{n-1}}}}$

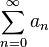is bounded, where $\Delta u_{n}$ is the forward difference. Then the series $\sum _{{n=0}}^{{\infty }}a_{n}$ converges if the series

$\sum _{{n=0}}^{{\infty }}{\Delta u_{n}}a_{{u_{n}}}=\sum _{{n=0}}^{{\infty }}(u_{{n+1}}-u_{n})a_{{u_{n}}}$

converges.

Taking 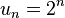$u_{n}=2^{n}$ , we see $\Delta u_{n}=2^{n}$ , so the Cauchy condensation test emerges as a special case.

References

Bonar, Khoury (2006). Real Infinite Series. Mathematical Association of America. ISBN 0-88385-745-6.

External links

Cauchy condensation test proof

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.