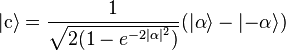Cat state

From Wikipedia, the free encyclopedia

In quantum computing, the cat state, named after Schrödinger's cat,[1] is the special pure quantum state where the qubits are in an equal superposition of all being |0⟩ and all being |1⟩, i.e. (in Bra-ket notation): |00⋯0⟩ + |11⋯1⟩.

In other quantum mechanics contexts, according to The New York Times for example, physicists view the cat state as composed of two diametrically opposed conditions at the same time,[2] such as the possibilities that a cat be alive and dead at the same time. This is sometimes connected to the many worlds hypothesis by proponents of the many worlds interpretation of quantum mechanics. More prosaically, a cat state might be the possibilities that six atoms be spin up and spin down, as published by a team at NIST, December 1, 2005.[3] This spin up/down formulation was proposed by David Bohm, who conceived of spin as an observable in a version of thought experiments formulated in the 1935 EPR paradox.[4] David Bohm and Yakir Aharonov later attained recognition for the Aharonov–Bohm effect, 1959.

In quantum optics

In quantum optics, a cat state is defined as the coherent superposition of two coherent states with opposite phase:

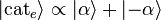|{\mathrm {cat}}_{e}\rangle \propto |\alpha \rangle +|{-}\alpha \rangle ,

where

|\alpha \rangle =e^{{-{|\alpha |^{2} \over 2}}}\sum _{{n=0}}^{{\infty }}{\alpha ^{n} \over {\sqrt {n!}}}|n\rangle ,

and

|{-}\alpha \rangle =e^{{-{|{-}\alpha |^{2} \over 2}}}\sum _{{n=0}}^{{\infty }}{({-}\alpha )^{n} \over {\sqrt {n!}}}|n\rangle ,

are coherent states defined in the number (Fock) basis. Notice that if we add the two states together, the resulting cat state only contains even Fock state terms

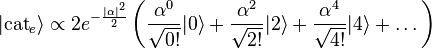|{\mathrm {cat}}_{e}\rangle \propto 2e^{{-{|\alpha |^{2} \over 2}}}\left({\alpha ^{0} \over {\sqrt {0!}}}|0\rangle +{\alpha ^{2} \over {\sqrt {2!}}}|2\rangle +{\alpha ^{4} \over {\sqrt {4!}}}|4\rangle +\dots \right).

As a result of this property, the above cat state is often referred to as an even cat state. Alternatively, we can define an odd cat state as

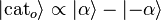|{\mathrm {cat}}_{o}\rangle \propto |\alpha \rangle -|{-}\alpha \rangle ,

which only contains odd Fock states

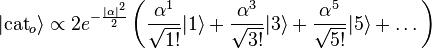|{\mathrm {cat}}_{o}\rangle \propto 2e^{{-{|\alpha |^{2} \over 2}}}\left({\alpha ^{1} \over {\sqrt {1!}}}|1\rangle +{\alpha ^{3} \over {\sqrt {3!}}}|3\rangle +{\alpha ^{5} \over {\sqrt {5!}}}|5\rangle +\dots \right).

Even and odd coherent states were first introduced by Dodonov, Malkin, and Man'ko in 1974.[5]

Linear superposition of coherent states

A simple example of a cat state is a linear superposition of coherent states with opposite phases, when each state has the same weight:

|{\mathrm {c}}\rangle ={\frac {1}{{\sqrt {2(1+e^{{-2|\alpha |^{2}}})}}}}(|\alpha \rangle +|{-}\alpha \rangle )
|{\mathrm {c}}\rangle ={\frac {1}{{\sqrt {2(1-e^{{-2|\alpha |^{2}}})}}}}(|\alpha \rangle -|{-}\alpha \rangle )

See also

The reading list contained in Incompleteness of quantum physics.

Notes

  1. ↑ John Gribbin (1984), In Search of Schrödinger's Cat, ISBN 0-552-12555-5, 22 February 1985, Transworld Publishers, Ltd, 318 pages.
  2. ↑ Dennis Overbye, "Quantum Trickery: Testing Einstein's Strangest Theory". New York Times Tuesday (Science Times), December 27, 2005 pages D1,D4.
  3. ↑ D. Leibfried, E. Knill, S. Seidelin, J. Britton, R.B. Blakestad, J. Chiaverini, D. Hume, W.M. Itano, J.D. Jost, C. Langer, R. Ozeri, R. Reichle, and D.J. Wineland. "Creation of a six atom 'Schrödinger cat' state". Nature. Dec. 1, 2005, 639–642.
  4. ↑ Amir D. Aczel (2001), Entanglement: the unlikely story of how scientists, mathematicians, and philosophers proved Einstein's spookiest theory. ISBN 0-452-28457-0 Penguin: paperback, 284 pages, index.
  5. ↑ V.V. Dodonov, I.A. Malkin, V.I. Man'ko. Physica, Volume 72, Issue 3, 15 March 1974, Pages 597–615.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.