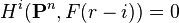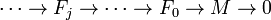Castelnuovo–Mumford regularity
In algebraic geometry, the Castelnuovo–Mumford regularity of a coherent sheaf F over projective space Pn is the smallest integer r such that it is r-regular, meaning that
whenever i > 0. The regularity of a subscheme is defined to be the regularity of its sheaf of ideals. The regularity controls when the Hilbert function of the sheaf becomes a polynomial; more precisely dim H0(Pn, F(m)) is a polynomial in m when m is at least the regularity. The concept of r-regularity was introduced by Mumford (1966, lecture 14), who attributed the following results to Guido Castelnuovo:
- An r-regular sheaf is s-regular for any s ≥ r.
- If a coherent sheaf is r-regular then F(r) is generated by its global sections.
Graded modules
A related idea exists in commutative algebra. Suppose R = k[x0,...,xn] is a polynomial ring over a field k and M is a finitely generated graded R-module. Suppose M has a minimal graded free resolution
and let bj be the maximum of the degrees of the generators of Fj. If r is an integer such that bj - j ≤ r for all j, then M is said to be r-regular. The regularity of M is the smallest such r.
These two notions of regularity coincide when F is a coherent sheaf such that Ass(F) contains no closed points. Then the graded module M=  d∈Z H0(Pn,F(d)) is finitely generated and has the same regularity as F.
d∈Z H0(Pn,F(d)) is finitely generated and has the same regularity as F.
References
- Eisenbud, David (1995), Commutative algebra with a view toward algebraic geometry, Graduate Texts in Mathematics 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94269-8, MR 1322960
- Eisenbud, David (2005), The geometry of syzygies, Graduate Texts in Mathematics 229, Berlin, New York: Springer-Verlag, doi:10.1007/b137572, ISBN 978-0-387-22215-8, MR 2103875
- Mumford, David (1966), Lectures on Curves on an Algebraic Surface, Annals of Mathematics Studies 59, Princeton University Press, ISBN 978-0-691-07993-6, MR 0209285