Cartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition or singular value decomposition of matrices. Its history can be traced to the 1880s work of Élie Cartan and Wilhelm Killing.
Cartan involutions on Lie algebras
Let  be a real semisimple Lie algebra and let
be a real semisimple Lie algebra and let 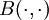 be its Killing form. An involution on
be its Killing form. An involution on  is a Lie algebra automorphism
is a Lie algebra automorphism 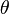 of
of  whose square is equal to the identity. Such an involution is called a Cartan involution on
whose square is equal to the identity. Such an involution is called a Cartan involution on  if
if 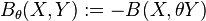 is a positive definite bilinear form.
is a positive definite bilinear form.
Two involutions  and
and 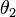 are considered equivalent if they differ only by an inner automorphism.
are considered equivalent if they differ only by an inner automorphism.
Any real semisimple Lie algebra has a Cartan involution, and any two Cartan involutions are equivalent.
Examples
- A Cartan involution on
 is defined by
is defined by  , where
, where 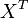 denotes the transpose matrix of
denotes the transpose matrix of  .
. - The identity map on
 is an involution, of course. It is the unique Cartan involution of
is an involution, of course. It is the unique Cartan involution of  if and only if the Killing form of
if and only if the Killing form of  is negative definite. Equivalently,
is negative definite. Equivalently,  is the Lie algebra of a compact semisimple Lie group.
is the Lie algebra of a compact semisimple Lie group. - Let
 be the complexification of a real semisimple Lie algebra
be the complexification of a real semisimple Lie algebra  , then complex conjugation on
, then complex conjugation on  is an involution on
is an involution on  . This is the Cartan involution on
. This is the Cartan involution on  if and only if
if and only if  is the Lie algebra of a compact Lie group.
is the Lie algebra of a compact Lie group. - The following maps are involutions of the Lie algebra
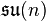 of the special unitary group SU(n):
of the special unitary group SU(n):
- the identity involution
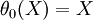 , which is the unique Cartan involution in this case;
, which is the unique Cartan involution in this case; -
 which on
which on 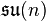 is also the complex conjugation;
is also the complex conjugation; - if
 is odd,
is odd,  . These are all equivalent, but not equivalent to the identity involution (because the matrix
. These are all equivalent, but not equivalent to the identity involution (because the matrix  does not belong to
does not belong to 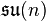 .)
.) - if
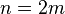 is even, we also have
is even, we also have 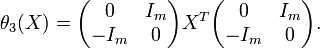
- the identity involution
Cartan pairs
Let 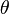 be an involution on a Lie algebra
be an involution on a Lie algebra  . Since
. Since 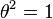 , the linear map
, the linear map 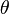 has the two eigenvalues
has the two eigenvalues 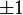 . Let
. Let 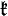 and
and  be the corresponding eigenspaces, then
be the corresponding eigenspaces, then 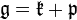 . Since
. Since 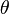 is a Lie algebra automorphism, eigenvalues are multiplicative. It follows that
is a Lie algebra automorphism, eigenvalues are multiplicative. It follows that
-
![[{\mathfrak {k}},{\mathfrak {k}}]\subseteq {\mathfrak {k}}](/2014-wikipedia_en_all_02_2014/I/media/9/c/2/4/9c245d0a6869cead06e0e7a90e959b15.png) ,
, ![[{\mathfrak {k}},{\mathfrak {p}}]\subseteq {\mathfrak {p}}](/2014-wikipedia_en_all_02_2014/I/media/7/2/8/3/72839dddfb35d8a3b7180f13bc3ca0cf.png) , and
, and ![[{\mathfrak {p}},{\mathfrak {p}}]\subseteq {\mathfrak {k}}](/2014-wikipedia_en_all_02_2014/I/media/8/4/0/7/8407a3bd251724fcdd7496cbc4fb280b.png) .
.
Thus 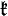 is a Lie subalgebra, while any subalgebra of
is a Lie subalgebra, while any subalgebra of  is commutative.
is commutative.
Conversely, a decomposition 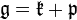 with these extra properties determines an involution
with these extra properties determines an involution 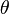 on
on  that is
that is 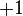 on
on 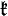 and
and  on
on  .
.
Such a pair  is also called a Cartan pair of
is also called a Cartan pair of  .
.
The decomposition 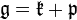 associated to a Cartan involution is called a Cartan decomposition of
associated to a Cartan involution is called a Cartan decomposition of  . The special feature of a Cartan decomposition is that the Killing form is negative definite on
. The special feature of a Cartan decomposition is that the Killing form is negative definite on 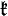 and positive definite on
and positive definite on  . Furthermore,
. Furthermore, 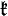 and
and  are orthogonal complements of each other with respect to the Killing form on
are orthogonal complements of each other with respect to the Killing form on  .
.
Cartan decomposition on the Lie group level
Let  be a semisimple Lie group and
be a semisimple Lie group and  its Lie algebra. Let
its Lie algebra. Let 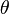 be a Cartan involution on
be a Cartan involution on  and let
and let  be the resulting Cartan pair. Let
be the resulting Cartan pair. Let  be the analytic subgroup of
be the analytic subgroup of  with Lie algebra
with Lie algebra 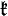 . Then:
. Then:
- There is a Lie group automorphism
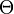 with differential
with differential 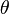 that satisfies
that satisfies  .
. - The subgroup of elements fixed by
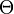 is
is  ; in particular,
; in particular,  is a closed subgroup.
is a closed subgroup. - The mapping
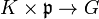 given by
given by  is a diffeomorphism.
is a diffeomorphism. - The subgroup
 contains the center
contains the center  of
of  , and
, and  is compact modulo center, that is,
is compact modulo center, that is,  is compact.
is compact. - The subgroup
 is the maximal subgroup of
is the maximal subgroup of  that contains the center and is compact modulo center.
that contains the center and is compact modulo center.
The automorphism 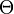 is also called global Cartan involution, and the diffeomorphism
is also called global Cartan involution, and the diffeomorphism 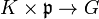 is called global Cartan decomposition.
is called global Cartan decomposition.
For the general linear group, we get  as the Cartan involution.
as the Cartan involution.
A refinement of the Cartan decomposition for symmetric spaces of compact or noncompact type states that the maximal Abelian subalgebras  in
in  are unique up to conjugation by K. Moreover
are unique up to conjugation by K. Moreover
In the compact and noncompact case this Lie algebraic result implies the decomposition
where A = exp  . Geometrically the image of the subgroup A in G / K ia a totally geodesic submanifold.
. Geometrically the image of the subgroup A in G / K ia a totally geodesic submanifold.
Relation to polar decomposition
Consider  with the Cartan involution
with the Cartan involution  . Then
. Then  is the real Lie algebra of skew-symmetric matrices, so that
is the real Lie algebra of skew-symmetric matrices, so that  , while
, while  is the subspace of symmetric matrices. Thus the exponential map is a diffeomorphism from
is the subspace of symmetric matrices. Thus the exponential map is a diffeomorphism from  onto the space of positive definite matrices. Up to this exponential map, the global Cartan decomposition is the polar decomposition of a matrix. Notice that the polar decomposition of an invertible matrix is unique.
onto the space of positive definite matrices. Up to this exponential map, the global Cartan decomposition is the polar decomposition of a matrix. Notice that the polar decomposition of an invertible matrix is unique.
See also
- Lie group decompositions
References
- Helgason, Sigurdur (1978), Differential geometry, Lie groups, and symmetric spaces, Academic Press, ISBN 0-8218-2848-7
- A. W. Knapp, Lie groups beyond an introduction, ISBN 0-8176-4259-5, Birkhäuser.

