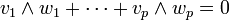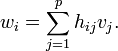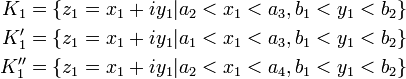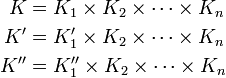Cartan's lemma

From Wikipedia, the free encyclopedia

In mathematics, Cartan's lemma refers to a number of results named after either Élie Cartan or his son Henri Cartan:

In exterior algebra:^[1] Suppose that v₁, ..., v_p are linearly independent elements of a vector space V and w₁, ..., w_p are such that

$v_{1}\wedge w_{1}+\cdots +v_{p}\wedge w_{p}=0$

in ΛV. Then there are scalars h_ij = h_ji such that

$w_{i}=\sum _{{j=1}}^{p}h_{{ij}}v_{j}.$

In several complex variables:^[2] Let a₁ < a₂ < a₃ < a₄ and b₁ < b₂ and define rectangles in the complex plane C by

${\begin{aligned}K_{1}&=\{z_{1}=x_{1}+iy_{1}|a_{2}<x_{1}<a_{3},b_{1}<y_{1}<b_{2}\}\\K_{1}'&=\{z_{1}=x_{1}+iy_{1}|a_{1}<x_{1}<a_{3},b_{1}<y_{1}<b_{2}\}\\K_{1}''&=\{z_{1}=x_{1}+iy_{1}|a_{2}<x_{1}<a_{4},b_{1}<y_{1}<b_{2}\}\end{aligned}}$

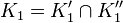so that $K_{1}=K_{1}'\cap K_{1}''$ . Let K₂, ..., K_n be simply connected domains in C and let

${\begin{aligned}K&=K_{1}\times K_{2}\times \cdots \times K_{n}\\K'&=K_{1}'\times K_{2}\times \cdots \times K_{n}\\K''&=K_{1}''\times K_{2}\times \cdots \times K_{n}\end{aligned}}$

so that again $K=K'\cap K''$ . Suppose that F(z) is a complex analytic matrix-valued function on a rectangle K in Cⁿ such that F(z) is an invertible matrix for each z in K. Then there exist analytic functions $F'\,$ in $K'\,$ and $F''\,$ in $K''\,$ such that

$F(z)=F'(z)/F''(z)\,$

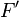in K.

In potential theory, a result that estimates the Hausdorff measure of the set on which a logarithmic Newtonian potential is small. See Cartan's lemma (potential theory).

References

↑
- Sternberg, S. (1983). Lectures on Differential Geometry ((2nd ed.) ed.). New York: Chelsea Publishing Co. p. 18. ISBN 0-8218-1385-4. OCLC 43032711.
↑ Robert C. Gunning and Hugo Rossi (1965). Analytic Functions of Several Complex Variables. Prentice-Hall.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.