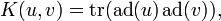Cartan's criterion
In mathematics, Cartan's criterion gives conditions for a Lie algebra in characteristic 0 to be solvable, which implies a related criterion for the Lie algebra to be semisimple. It is based on the notion of the Killing form, a symmetric bilinear form on  defined by the formula
defined by the formula
where tr denotes the trace of a linear operator. The criterion was introduced by Élie Cartan (1894).
Cartan's criterion for solvability
Cartan's criterion for solvability states:
- A Lie subalgebra
 of endomorphisms of a finite dimensional vector space over a field of characteristic zero is solvable if and only if
of endomorphisms of a finite dimensional vector space over a field of characteristic zero is solvable if and only if  whenever
whenever ![a\in {\mathfrak {g}},b\in [{\mathfrak {g}},{\mathfrak {g}}].](/2014-wikipedia_en_all_02_2014/I/media/9/f/b/2/9fb2c7648fe4e9d81cf56295a2dbb56e.png)
The fact that  in the solvable case follows immediately from Lie's theorem that solvable Lie algebras in characteristic 0 can be put in upper triangular form.
in the solvable case follows immediately from Lie's theorem that solvable Lie algebras in characteristic 0 can be put in upper triangular form.
Applying Cartan's criterion to the adjoint representation gives:
- A finite-dimensional Lie algebra
 over a field of characteristic zero is solvable if and only if
over a field of characteristic zero is solvable if and only if ![K({\mathfrak {g}},[{\mathfrak {g}},{\mathfrak {g}}])=0](/2014-wikipedia_en_all_02_2014/I/media/6/1/3/3/61338bce9b51a07b68a3cea22d3de6f1.png) (where K is the Killing form).
(where K is the Killing form).
Cartan's criterion for semisimplicity
Cartan's criterion for semisimplicity states:
- A finite-dimensional Lie algebra
 over a field of characteristic zero is semisimple if and only if the Killing form is non-degenerate.
over a field of characteristic zero is semisimple if and only if the Killing form is non-degenerate.
Dieudonné (1953) gave a very short proof that if a finite dimensional Lie algebra (in any characteristic) has a non-degenerate invariant bilinear form and no non-zero abelian ideals, and in particular if its Killing form is non-degenerate, then it is a sum of simple Lie algebras.
Conversely, it follows easily from Cartan's criterion for solvability that a semisimple algebra (in characteristic 0) has a non-degenerate Killing form.
Examples
Cartan's criteria fail in characteristic p>0; for example:
- the Lie algebra SLp(k) is simple if k has characteristic not 2 and has vanishing Killing form, though it does have a nonzero invariant bilinear form given by (a,b) = Tr(ab).
- the Lie algebra with basis an for n∈Z/pZ and bracket [ai,aj] = (i−j)ai+j is simple for p>2 but has no nonzero invariant bilinear form.
- If k has characteristic 2 then the semidirect product gl2(k).k2 is a solvable Lie algebra, but the Killing form is not identically zero on its derived algebra sl2(k).k2.
If a finite dimensional Lie algebra is nilpotent, then the Killing form is identically zero (and more generally the Killing form vanishes on any nilpotent ideal). The converse is false: there are non-nilpotent Lie algebras whose Killing form vanishes. An example is given by the semidirect product of an abelian Lie algebra V with a 1-dimensional Lie algebra acting on V as an endomorphism b such that b is not nilpotent and Tr(b2)=0.
In characteristic 0, every reductive Lie algebra (one that is a sum of abelian and simple Lie algebras) has a non-degenerate invariant symmetric bilinear form. However the converse is false: a Lie algebra with a non-degenerate invariant symmetric bilinear form need not be a sum of simple and abelian Lie algebras. A typical counterexample is G = L[t]/tnL[t] where n>1, L is a simple complex Lie algebra with a bilinear form (,), and the bilinear form on G is given by taking the coefficient of tn−1 of the C[t]-valued bilinear form on G induced by the form on L. The bilinear form is non-degenerate, but the Lie algebra is not a sum of simple and abelian Lie algebras.
References
- Cartan, Élie (1894), Sur la structure des groupes de transformations finis et continus, Thesis, Nony
- Dieudonné, Jean (1953), "On semi-simple Lie algebras", Proceedings of the American Mathematical Society 4: 931–932, ISSN 0002-9939, JSTOR 2031832, MR 0059262
- Serre, Jean-Pierre (2006) [1964], Lie algebras and Lie groups, Lecture Notes in Mathematics 1500, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-540-70634-2, ISBN 978-3-540-55008-2, MR 2179691