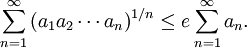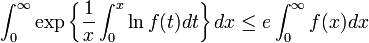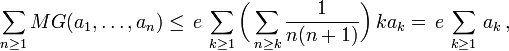Carleman's inequality

From Wikipedia, the free encyclopedia

Carleman's inequality is an inequality in mathematics, named after Torsten Carleman, who proved it in 1923^[1] and used it to prove the Denjoy–Carleman theorem on quasi-analytic classes.^[2]^[3]

Statement

Let a₁, a₂, a₃, ... be a sequence of non-negative real numbers, then

$\sum _{{n=1}}^{\infty }\left(a_{1}a_{2}\cdots a_{n}\right)^{{1/n}}\leq e\sum _{{n=1}}^{\infty }a_{n}.$

The constant e in the inequality is optimal, that is, the inequality does not always hold if e is replaced by a smaller number. The inequality is strict (it holds with "<" instead of "≤") if some element in the sequence is non-zero.

Integral version

Carleman's inequality has an integral version, which states that

$\int _{0}^{\infty }\exp \left\{{\frac {1}{x}}\int _{0}^{x}\ln f(t)dt\right\}dx\leq e\int _{0}^{\infty }f(x)dx$

for any f ≥ 0.

Carleson's inequality

A generalisation, due to Lennart Carleson, states the following:^[4]

for any convex function g with g(0) = 0, and for any -1 < p < ∞,

$\int _{0}^{\infty }x^{p}e^{{-g(x)/x}}dx\leq e^{{p+1}}\int _{0}^{\infty }x^{p}e^{{-g'(x)}}dx.\,$

Carleman's inequality follows from the case p = 0.

Proof

An elementary proof is sketched below. From the inequality of arithmetic and geometric means applied to the numbers 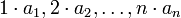$1\cdot a_{1},2\cdot a_{2},\dots ,n\cdot a_{n}$

${\mathrm {MG}}(a_{1},\dots ,a_{n})={\mathrm {MG}}(1a_{1},2a_{2},\dots ,na_{n})(n!)^{{-1/n}}\leq {\mathrm {MA}}(1a_{1},2a_{2},\dots ,na_{n})(n!)^{{-1/n}}\,$

where MG stands for geometric mean, and MA — for arithmetic mean. The Stirling-type inequality 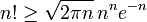$n!\geq {\sqrt {2\pi n}}\,n^{n}e^{{-n}}$ applied to $n+1$ implies

$(n!)^{{-1/n}}\leq {\frac {e}{n+1}}$ for all $n\geq 1.$

Therefore

$MG(a_{1},\dots ,a_{n})\leq {\frac {e}{n(n+1)}}\,\sum _{{1\leq k\leq n}}ka_{k}\,,$

whence

$\sum _{{n\geq 1}}MG(a_{1},\dots ,a_{n})\leq \,e\,\sum _{{k\geq 1}}{\bigg (}\sum _{{n\geq k}}{\frac {1}{n(n+1)}}{\bigg )}\,ka_{k}=\,e\,\sum _{{k\geq 1}}\,a_{k}\,,$

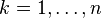proving the inequality. Moreover, the inequality of arithmetic and geometric means of $n$ non-negative numbers is known to be an equality if and only if all the numbers coincide, that is, in the present case, if and only if $a_{k}=C/k$ for $k=1,\dots ,n$ . As a consequence, Carleman's inequality is never an equality for a convergent series, unless all $a_{n}$ vanish, just because the harmonic series is divergent.

One can also prove Carleman's inequality by starting with Hardy's inequality

$\sum _{{n=1}}^{\infty }\left({\frac {a_{1}+a_{2}+\cdots +a_{n}}{n}}\right)^{p}\leq \left({\frac {p}{p-1}}\right)^{p}\sum _{{n=1}}^{\infty }a_{n}^{p}$

for the non-negative numbers a₁,a₂,... and p > 1, replacing each a_n with a1/p
n, and letting p → ∞.

Notes

↑ T. Carleman, Sur les fonctions quasi-analytiques, Conférences faites au cinquième congres des mathématiciens Scandinaves, Helsinki (1923), 181-196.
↑ Duncan, John; McGregor, Colin M. (2003). "Carleman's inequality". Amer. Math. Monthly 110 (5): 424–431. MR 2040885.
↑ Pečarić, Josip; Stolarsky, Kenneth B. (2001). "Carleman's inequality: history and new generalizations". Aequationes Math. 61 (1–2): 49–62. MR 1820809.
↑ Carleson, L. (1954). "A proof of an inequality of Carleman". Proc. Amer. Math. Soc. 5: 932–933.

References

Hardy, G. H.; Littlewood. J.E.; Pólya, G. (1952). Inequalities, 2nd ed. Cambridge University Press. ISBN 0-521-35880-9. Cite uses deprecated parameters (help)
Rassias, Thermistocles M., editor (2000). Survey on classical inequalities. Kluwer Academic. ISBN 0-7923-6483-X.
Hörmander, Lars (1990). The analysis of linear partial differential operators I: distribution theory and Fourier analysis, 2nd ed. Springer. ISBN 3-540-52343-X.

External links

Hazewinkel, Michiel, ed. (2001), "Carleman inequality", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.