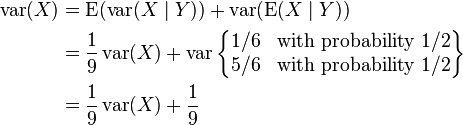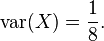Cantor distribution

From Wikipedia, the free encyclopedia

Cantor
Parameters	none
Support	Cantor set
pmf	none
CDF	Cantor function
Mean	1/2
Median	anywhere in [1/3, 2/3]
Mode	n/a
Variance	1/8
Skewness	0
Ex. kurtosis	−8/5
MGF	$e^{{t/2}}\prod _{{i=1}}^{{\infty }}\cosh {\left({\frac {t}{3^{{i}}}}\right)}$
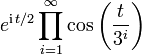CF	$e^{{{\mathrm {i}}\,t/2}}\prod _{{i=1}}^{{\infty }}\cos {\left({\frac {t}{3^{{i}}}}\right)}$

The Cantor distribution is the probability distribution whose cumulative distribution function is the Cantor function.

This distribution has neither a probability density function nor a probability mass function, as it is not absolutely continuous with respect to Lebesgue measure, nor has it any point-masses. It is thus neither a discrete nor an absolutely continuous probability distribution, nor is it a mixture of these. Rather it is an example of a singular distribution.

Its cumulative distribution function is sometimes referred to as the Devil's staircase, although that term has a more general meaning.

Characterization

The support of the Cantor distribution is the Cantor set, itself the intersection of the (countably infinitely many) sets

${\begin{aligned}C_{{0}}=&[0,1]\\C_{{1}}=&[0,1/3]\cup [2/3,1]\\C_{{2}}=&[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1]\\C_{{3}}=&[0,1/27]\cup [2/27,1/9]\cup [2/9,7/27]\cup [8/27,1/3]\cup \\&[2/3,19/27]\cup [20/27,7/9]\cup [8/9,25/27]\cup [26/27,1]\\C_{{4}}=&\cdots .\end{aligned}}$

The Cantor distribution is the unique probability distribution for which for any C_t (t ∈ { 0, 1, 2, 3, ... }), the probability of a particular interval in C_t containing the Cantor-distributed random variable is identically 2^-t on each one of the 2^t intervals.

Moments

It is easy to see by symmetry that for a random variable X having this distribution, its expected value E(X) = 1/2, and that all odd central moments of X are 0.

The law of total variance can be used to find the variance var(X), as follows. For the above set C₁, let Y = 0 if X ∈ [0,1/3], and 1 if X ∈ [2/3,1]. Then:

${\begin{aligned}\operatorname {var}(X)&=\operatorname {E}(\operatorname {var}(X\mid Y))+\operatorname {var}(\operatorname {E}(X\mid Y))\\&={\frac {1}{9}}\operatorname {var}(X)+\operatorname {var}\left\{{\begin{matrix}1/6&{\mbox{with probability}}\ 1/2\\5/6&{\mbox{with probability}}\ 1/2\end{matrix}}\right\}\\&={\frac {1}{9}}\operatorname {var}(X)+{\frac {1}{9}}\end{aligned}}$

From this we get:

$\operatorname {var}(X)={\frac {1}{8}}.$

A closed-form expression for any even central moment can be found by first obtaining the even cumulants

$\kappa _{{2n}}={\frac {2^{{2n-1}}(2^{{2n}}-1)B_{{2n}}}{n\,(3^{{2n}}-1)}},\,\!$

where B_2n is the 2nth Bernoulli number, and then expressing the moments as functions of the cumulants.

References

External links

Morrison, Kent (1998-07-23). "Random Walks with Decreasing Steps". Department of Mathematics, California Polytechnic State University. Retrieved 2007-02-16.

Probability distributions

Discrete univariate with finite support

Benford Bernoulli Beta-binomial binomial categorical hypergeometric Poisson binomial Rademacher discrete uniform Zipf Zipf–Mandelbrot

Discrete univariate with infinite support

beta negative binomial Borel Conway–Maxwell–Poisson discrete phase-type Delaporte extended negative binomial Gauss–Kuzmin geometric logarithmic negative binomial parabolic fractal Poisson Skellam Yule–Simon zeta

Continuous univariate supported on a bounded interval, e.g. [0,1]

Arcsine ARGUS Balding–Nichols Bates Beta Beta rectangular Irwin–Hall Kumaraswamy logit-normal Noncentral beta raised cosine Triangular U-quadratic uniform Wigner semicircle Xenakis

[[List of probability distributions#Supported_on_semi-infinite_intervals.2C_usually_.5B0.2C.E2.88.9E.29|Continuous univariate supported on a semi-infinite interval, usually [0,∞)]]

Benini
Benktander 1st kind
Benktander 2nd kind
Beta prime
Burr
chi-squared
chi
Coxian
Dagum
Davis
EL
Erlang
exponential
F
folded normal
Flory-Schulz
Fréchet
Gamma
Gamma/Gompertz
generalized inverse Gaussian
Gompertz
half-logistic
half-normal
Hotelling's T-squared
hyper-Erlang
hyperexponential
hypoexponential
inverse chi-squared (scaled inverse chi-squared)
inverse Gaussian
inverse gamma
Kolmogorov
Lévy
log-Cauchy
log-Laplace
log-logistic
log-normal
Maxwell–Boltzmann
Maxwell–Jüttner
Mittag–Leffler
Nakagami
noncentral chi-squared
Pareto
phase-type
Poly-Weibull
Rayleigh
relativistic Breit–Wigner
Rice
Rosin–Rammler
shifted Gompertz
truncated normal
type-2 Gumbel
Weibull
Wilks' lambda

Continuous univariate supported on the whole real line (−∞, ∞)

Cauchy exponential power Fisher's z generalized normal generalized hyperbolic geometric stable Gumbel Holtsmark hyperbolic secant Johnson SU Landau Laplace Linnik logistic noncentral t normal (Gaussian) normal-inverse Gaussian skew normal slash stable Student's t type-1 Gumbel variance-gamma Voigt

Continuous univariate with support whose type varies

generalized extreme value generalized Pareto Tukey lambda q-Gaussian q-exponential shifted log-logistic

Mixed continuous-discrete univariate distributions

rectified Gaussian

Multivariate (joint)

Discrete Ewens multinomial Dirichlet-multinomial negative multinomial Continuous Dirichlet Generalized Dirichlet multivariate normal Multivariate stable multivariate Student normal-scaled inverse gamma normal-gamma Matrix-valued inverse matrix gamma inverse-Wishart matrix normal matrix t matrix gamma normal-inverse-Wishart normal-Wishart Wishart

Directional

Univariate (circular) directional Circular uniform univariate von Mises wrapped normal wrapped Cauchy wrapped exponential wrapped Lévy Bivariate (spherical) Kent Bivariate (toroidal) bivariate von Mises Multivariate von Mises–Fisher Bingham

Degenerate and singular

Degenerate discrete degenerate Dirac delta function Singular Cantor

Families

Circular compound Poisson elliptical exponential natural exponential location-scale maximum entropy mixture Pearson Tweedie wrapped

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.