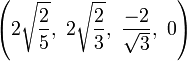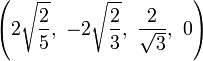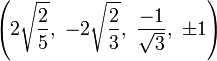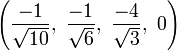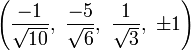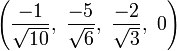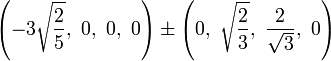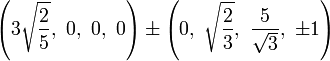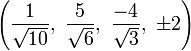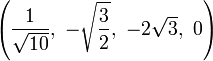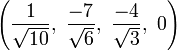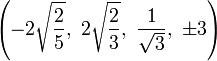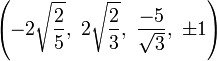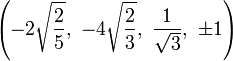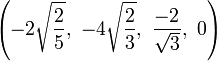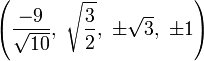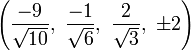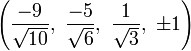Cantellated 5-cell
 5-cell |
 Cantellated 5-cell |
 Cantitruncated 5-cell |
| Orthogonal projections in A4 Coxeter plane | ||
|---|---|---|
In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation (a 2nd order truncation) of the regular 5-cell.
There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.
Cantellation 5-cell
| Cantellated 5-cell | ||
|---|---|---|
 Schlegel diagram with octahedral cells shown | ||
| Type | Uniform polychoron | |
| Schläfli symbol | t0,2{3,3,3} | |
| Coxeter-Dynkin diagram | ||
| Cells | 20 | 5 5 10 |
| Faces | 80 | 50{3} 30{4} |
| Edges | 90 | |
| Vertices | 30 | |
| Vertex figure |  Irreg. triangular prism | |
| Symmetry group | A4, [3,3,3], order 120 | |
| Properties | convex, isogonal | |
| Uniform index | 3 4 5 | |
The cantellated 5-cell is a uniform polychoron. It has 30 vertices, 90 edges, 80 faces, and 20 cells. The cells are 5 cuboctahedra, 5 octahedra, and 10 triangular prisms. Each vertex is surrounded by 2 cuboctahedra, 2 triangular prisms, and 1 octahedron; the vertex figure is a nonuniform triangular prism.
Alternate names
- Cantellated pentachoron
- Cantellated 4-simplex
- (small) prismatodispentachoron
- Rectified dispentachoron
- Small rhombated pentachoron (Acronym: Srip) (Jonathan Bowers)
Images
| Ak Coxeter plane |
A4 | A3 | A2 |
|---|---|---|---|
| Graph |  |
 |
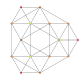 |
| Dihedral symmetry | [5] | [4] | [3] |
 Wireframe |
 Ten triangular prisms colored green |
 Five octahedra colored blue |
Coordinates
The Cartesian coordinates of the vertices of the origin-centered cantellated 5-cell having edge length 2 are:
|
|
|
The vertices of the cantellated 5-cell can be most simply positioned in 5-space as permutations of:
- (0,0,1,1,2)
This construction is from the positive orthant facet of the cantellated 5-orthoplex.
Cantitruncated 5-cell
| Cantitruncated 5-cell | ||
|---|---|---|
 Schlegel diagram with Truncated tetrahedral cells shown | ||
| Type | Uniform polychoron | |
| Schläfli symbol | t0,1,2{3,3,3} | |
| Coxeter-Dynkin diagram | ||
| Cells | 20 | 5 10 5 |
| Faces | 80 | 20{3} 30{4} 30{6} |
| Edges | 120 | |
| Vertices | 60 | |
| Vertex figure |  sphenoid | |
| Symmetry group | A4, [3,3,3], order 120 | |
| Properties | convex, isogonal | |
| Uniform index | 6 7 8 | |
The cantitruncated 5-cell is a uniform polychoron. It is composed of 60 vertices, 120 edges, 80 faces, and 20 cells. The cells are: 5 truncated octahedra, 10 triangular prisms, and 5 truncated tetrahedra. Each vertex is surrounded by 2 truncated octahedra, one triangular prism, and one truncated tetrahedron.
Alternative names
- Cantitruncated pentachoron
- Cantitruncated 4-simplex
- Great prismatodispentachoron
- Truncated dispentachoron
- Great rhombated pentachoron (Acronym: grip) (Jonathan Bowers)
Images
| Ak Coxeter plane |
A4 | A3 | A2 |
|---|---|---|---|
| Graph |  |
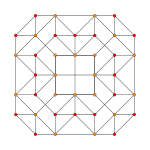 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
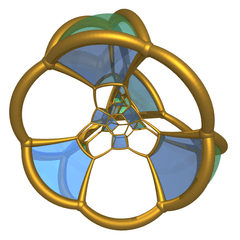 Stereographic projection with its 10 triangular prisms. |
Cartesian coordinates
The Cartesian coordinates of an origin-centered cantitruncated 5-cell having edge length 2 are:
|
|
|
These vertices can be more simply constructed on a hyperplane in 5-space, as the permutations of:
- (0,0,1,2,3)
This construction is from the positive orthant facet of the cantitruncated 5-orthoplex.
Related polychora
These polytopes are art of a set of 9 uniform polychora constructed from the [3,3,3] Coxeter group.
| Name | 5-cell | truncated 5-cell | rectified 5-cell | cantellated 5-cell | bitruncated 5-cell | cantitruncated 5-cell | runcinated 5-cell | runcitruncated 5-cell | omnitruncated 5-cell |
|---|---|---|---|---|---|---|---|---|---|
| Schläfli symbol |
{3,3,3} | t0,1{3,3,3} | t1{3,3,3} | t0,2{3,3,3} | t1,2{3,3,3} | t0,1,2{3,3,3} | t0,3{3,3,3} | t0,1,3{3,3,3} | t0,1,2,3{3,3,3} |
| Coxeter-Dynkin diagram |
|||||||||
| Schlegel diagram |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| A4 Coxeter plane Graph |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| A3 Coxeter plane Graph |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| A2 Coxeter plane Graph |
 |
 |
 |
 |
 |
 |
 |
 |
 |
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- 1. Convex uniform polychora based on the pentachoron - Model 4, 7, George Olshevsky.
- Richard Klitzing, 4D, uniform polytopes (polychora) x3o3x3o - srip, x3x3x3o - grip
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | BCn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes | ||||||||||||