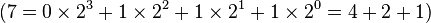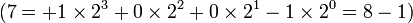Canonical signed digit

From Wikipedia, the free encyclopedia

In computing canonical-signed-digit (CSD) is a number system for encoding a floating-point value in a two's complement representation. This encoding contains 33% fewer non-zeros than the two's complement form, leading to efficient implementations of add/subtract networks in hardwired Digital signal processing.

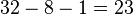
The representation uses a sequence of one or more of the symbols, -1, 0, +1 (alternatively -, 0 or +) with each position possibly representing the addition or subtraction of a power of 2. For instance 23 is represented as +0-00-, which expands to $+2^{5}-2^{3}-2^{0}$ or $32-8-1=23$

Implementation

CSD is obtained by transforming every sequence of zero followed by ones (011...1) into + followed by zeros and the least significant bit by - (+0....0-).

As an example: the number 7 has a two's complement representation 0111

$(7=0\times 2^{3}+1\times 2^{2}+1\times 2^{1}+1\times 2^{0}=4+2+1)$

into +00-

$(7=+1\times 2^{3}+0\times 2^{2}+0\times 2^{1}-1\times 2^{0}=8-1)$

External links

"Fractions in the Canonical-Signed-Digit Number System". CiteSeerX: 10.1.1.126.5477. Missing or empty |url= (help)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.