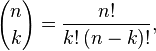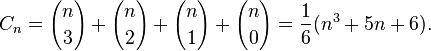Cake number

From Wikipedia, the free encyclopedia

In mathematics, the cake number, denoted by Cn, is the maximum number of regions into which a 3-dimensional cube can be partitioned by exactly n planes. The cake number is so-called because one may imagine each partition of the cube by a plane as a slice made by a knife through a cube-shaped cake.

The values of Cn for increasing n ≥ 0 are given by 1, 2, 4, 8, 15, 26, 42, 64, 93, …[1]

The cake numbers are the 3-dimensional analogue of the 2-dimensional lazy caterer's sequence; the difference between successive cake numbers also gives the lazy caterer's sequence.

General formula

If n! denotes the factorial, and we denote the binomial coefficients by

{n \choose k}={\frac {n!}{k!\,(n-k)!}},

and we assume that n planes are available to partition the cube, then the number is:[2]

C_{n}={n \choose 3}+{n \choose 2}+{n \choose 1}+{n \choose 0}={\frac {1}{6}}(n^{3}+5n+6).

References

  1. ↑ The On-Line Encyclopedia of Integer Sequences. "A000125: Cake Numbers". Retrieved August 19, 2010. 
  2. ↑ Eric Weisstein. "Space Division by Planes". MathWorld − A Wolfram Web Resource. Retrieved August 19, 2010. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.