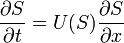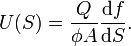Buckley–Leverett equation

From Wikipedia, the free encyclopedia

In fluid dynamics, the Buckley–Leverett equation is a transport equation used to model two-phase flow in porous media.[1] The Buckley–Leverett equation or the Buckley–Leverett displacement can be interpreted as a way of incorporating the microscopic effects due to capillary pressure in two-phase flow into Darcy's law.

In a 1D sample (control volume), let 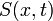S(x,t) be the water saturation, then the Buckley–Leverett equation is

{\frac {\partial S}{\partial t}}=U(S){\frac {\partial S}{\partial x}}

where

U(S)={\frac {Q}{\phi A}}{\frac {{\mathrm {d}}f}{{\mathrm {d}}S}}.

f is the fractional flow rate, Q is the total flow, \phi is porosity and A is area of the cross-section in the sample volume.

Assumptions for validity

The Buckley–Leverett equation is derived for a 1D sample given

  • mass conservation
  • capillary pressure 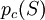p_{c}(S) is a function of water saturation 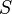S only
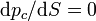  • {\mathrm {d}}p_{c}/{\mathrm {d}}S=0 causing the pressure gradients of the two phases to be equal.
  • Flow is Linear
  • Flow is Steady-State
  • Formation is one Layer

General solution

The solution of the Buckley–Leverett equation has the form 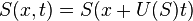S(x,t)=S(x+U(S)t) which means that 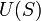U(S) is the front velocity of the fluids at saturation S.

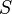See also

References

  1. ↑ S.E. Buckley and M.C. Leverett (1942). "Mechanism of fluid displacements in sands". Transactions of the AIME (146): 107–116. 


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.