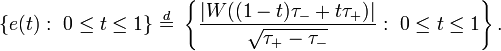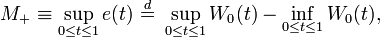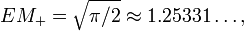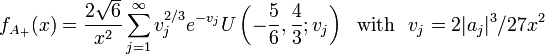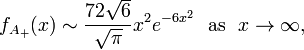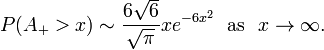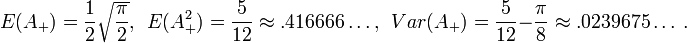Brownian excursion
In probability theory a Brownian excursion process is a stochastic processes that is closely related to a Wiener process (or Brownian motion). Realisations of Brownian excursion processes are essentially just realizations of a Wiener process selected to satisfy certain conditions. In particular, a Brownian excursion process is a Wiener process conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive. BEPs are important because, among other reasons, they naturally arise as the limit process of a number of conditional functional central limit theorems.[1]
Definition
A Brownian excursion process,  , is a Wiener process (or Brownian motion) conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive.
, is a Wiener process (or Brownian motion) conditioned to be positive and to take the value 0 at time 1. Alternatively, it is a Brownian bridge process conditioned to be positive.
Another representation of a Brownian excursion  in terms of a Brownian motion process W (due to Paul Lévy and noted by Kiyoshi Itō and Henry P. McKean, Jr.[2])
is in terms of the last time
in terms of a Brownian motion process W (due to Paul Lévy and noted by Kiyoshi Itō and Henry P. McKean, Jr.[2])
is in terms of the last time 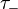 that W hits zero before time 1 and the first time
that W hits zero before time 1 and the first time  that Brownian motion
that Brownian motion 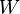 hits zero after time 1:[2]
hits zero after time 1:[2]
Let 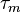 be the time that a
Brownian bridge process
be the time that a
Brownian bridge process 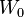 achieves its minimum on [0, 1]. Vervaat (1979) shows that
achieves its minimum on [0, 1]. Vervaat (1979) shows that
Properties
Vervaat's representation of a Brownian excursion has several consequences for various functions of  . In particular:
. In particular:
(this can also be derived by explicit calculations[3][4]) and
The following result holds:[5]
and the following values for the second moment and variance can be calculated by the exact form of the distribution and density:[5]
Groeneboom (1989), Lemma 4.2 gives an expression for the Laplace transform of (the density) of
 . A formula for a certain double transform of the distribution of
this area integral is given by Louchard (1984).
. A formula for a certain double transform of the distribution of
this area integral is given by Louchard (1984).
Groeneboom (1983) and Pitman (1983) give decompositions of Brownian motion 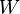 in terms of i.i.d Brownian excursions
and the least concave majorant (or greatest convex minorant) of
in terms of i.i.d Brownian excursions
and the least concave majorant (or greatest convex minorant) of 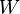 .
.
For an introduction to Itô's general theory of Brownian excursions and the Itô Poisson process of excursions, see Revuz and Yor (1994), chapter XII.
Connections and applications
The Brownian excursion area
arises in connection with the enumeration of connected graphs, many other problems in combinatorial theory; see e.g.
,[6]
,[7]
,[8]
,[9]
,[10]
and the limit distribution of the Betti numbers of certain varieties in cohomology theory
.[11]
Takacs (1991a) shows that 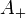 has density
has density
where  are the zeros of the Airy function and
are the zeros of the Airy function and  is the confluent hypergeometric function.
Janson and Louchard (2007) show that
is the confluent hypergeometric function.
Janson and Louchard (2007) show that
and
They also give higher-order expansions in both cases.
Janson (2007) gives moments of 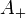 and many other area functionals. In particular,
and many other area functionals. In particular,
Brownian excursions also arise in connection with queuing problems,[12] railway traffic,[13][14] and the heights of random rooted binary trees.[15]
Related processes
- Brownian bridge
- Brownian meander
- reflected Brownian motion
- skew Brownian motion
Notes
- ↑ Durrett, Iglehart: Functionals of Brownian Meander and Brownian Excursion, (1975)
- ↑ 2.0 2.1 Itô and McKean (1974, page 75)
- ↑ Chung (1976)
- ↑ Kennedy (1976)
- ↑ 5.0 5.1 Durrett and Iglehart (1977)
- ↑ Wright, E. M. (1977). The number of connected sparsely edged graphs. J. Graph Th. 1, 317–330.
- ↑ Wright, E. M. (1980). The number connected sparsely edged graphs. III. Asymptotic results. J. Graph Th. 4, 393–407
- ↑ Spencer, J. (1997). Enumerating graphs and Brownian motion. Comm. Pure Appl. Math. 50, 291–294.
- ↑ Janson, S. (2007). Brownian excursion area, Wright's constants in graph enumeration, and other Brownian areas.
- ↑ Flajolet, P. and Louchard, G. (2001). Analytic variations on the Airy distribution. Algorithmica 31, 361–377.
- ↑ Reineke, M. (2005). Cohomology of noncommutative Hilbert schemes. Algebras and Representation Theory 8, 541–561.
- ↑ Iglehart, D. L. (1974). "Functional central limit theorms for random walks conditioned to stay positive." Ann. Probab., 2, 608–619.
- ↑ Takacs, L. (1991a). A Bernoulli excursion and its various applications. Adv. in Appl. Probab. 23, 557–585.
- ↑ Takacs, L. (1991b). "On a probability problem connected with railway traffic". J. Appl. Math. Stochastic Anal., 4, 263–292.
- ↑ Takacs, L. (1994). "On the total heights of rooted binary trees". J. Combin. Theory Ser. B, 61, 155–166.
References
- Chung, K. L. (1975). "Maxima in Brownian excursions". Bull. Amer. Math Soc. 81: 742–745. MR 0373035.
- Chung, K. L. (1976). "Excursions in Brownian motion". Arkiv för Matematik 14: 155–177. MR 0467948.
- Durrett, Richard T.; Iglehart, Donald L. (1977). "Functionals of Brownian meander and Brownian excursion". Annals of Probability 5: 130–135. JSTOR 2242808. MR 0436354.
- Groeneboom, Piet (1983). "The concave majorant of Brownian motion". Annals of Probability 11: 1016–1027. JSTOR 2243513. MR 714964.
- Groeneboom, Piet (1989). "Brownian motion with a parabolic drift and Airy functions". Probability Theory and Related Fields 81: 79–109. doi:10.1007/BF00343738. MR 981568.
- Itô, Kiyosi; McKean, Jr., Henry P. (2013) [1974]. Diffusion Processes and their Sample Paths. Classics in Mathematics (Second printing, corrected ed.). Springer-Verlag, Berlin. ISBN 978-3540606291. MR 0345224.
- Janson, Svante (2007). "Brownian excursion area, Wright's constants in graph enumeration, and other Brownian areas". Probability Surveys 4: 80–145. MR 2318402.
- Janson, Svante; Louchard, Guy (2007). "Tail estimates for the Brownian excursion area and other Brownian areas.". Electronic Journal of Probability 12: 1600–1632. MR 2365879.
- Kennedy, Douglas P. (1976). "The distribution of the maximum Brownian excursion". J. Appl. Probability 13: 371–376. JSTOR 3212843. MR 402955 A.
- Lévy, Paul (1948). Processus Stochastiques et Mouvement Brownien. Gauthier-Villars, Paris. MR 0029120.
- Louchard, G. (1984). "Kac's formula, Levy's local time and Brownian excursion". J. Appl. Probability 21: 479–499. JSTOR 3213611. MR 752014.
- Pitman, J. W. (1983). "Remarks on the convex minorant of Brownian motion". {Seminar on stochastic processes, 1982}. Progr. Probab. Statist. 5. Birkhauser, Boston. pp. 219–227. MR 733673.
- Revuz, Daniel; Yor, Marc (2004). Continuous Martingales and Brownian Motion. Grundlehren der mathematischen Wissenschaften (Book 293). Springer-Verlag, Berlin. MR 1725357.
- Vervaat, W. (1979). "A relation between Brownian bridge and Brownian excursion". Annals of Probability 7: 143–149. JSTOR 2242845. MR 515820.