Brocard's conjecture

From Wikipedia, the free encyclopedia

In number theory, Brocard's conjecture is a conjecture that there are at least four prime numbers between (p_n)² and (p_n+1)², for n > 1, where p_n is the n^th prime number.^[1] It is widely believed that this conjecture is true. However, it remains unproven as of January 2014.

n	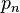$p_{n}$	$p_{n}^{2}$	Prime numbers	$\Delta$
1	2	4	5, 7	2
2	3	9	11, 13, 17, 19, 23	5
3	5	25	29, 31, 37, 41, 43, 47	6
4	7	49	53, 59, 61, 67, 71…	15
5	11	121	127, 131, 137, 139, 149…	9
$\Delta$ stands for $\pi (p_{{n+1}}^{2})-\pi (p_{n}^{2})$ .

The number of primes between prime squares is 2, 5, 6, 15, 9, 22, 11, 27, ... A050216.

Legendre's conjecture that there is a prime between consecutive integer squares directly implies that there are at least two primes between prime squares for p_n ≥ 3 since p_n+1 - p_n ≥ 2.

Notes

↑ Weisstein, Eric W., "Brocard's Conjecture", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.