Brillouin zone

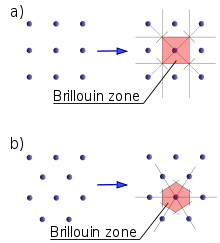
From Wikipedia, the free encyclopedia
The reciprocal lattices (dots) and corresponding first Brillouin zones of (a) square lattice and (b) hexagonal lattice.

Taking surfaces at the same distance from one element of the lattice and its neighbours, the volume included is the first Brillouin zone (see the derivation of the Wigner-Seitz cell). Another definition is as the set of points in k-space that can be reached from the origin without crossing any Bragg plane. Equivalently, this is the Voronoi cell around the origin of the reciprocal lattice.

There are also second, third, etc., Brillouin zones, corresponding to a sequence of disjoint regions (all with the same volume) at increasing distances from the origin, but these are used less frequently. As a result, the first Brillouin zone is often called simply the Brillouin zone. (In general, the n-th Brillouin zone consists of the set of points that can be reached from the origin by crossing exactly n − 1 distinct Bragg planes.)

A related concept is that of the irreducible Brillouin zone, which is the first Brillouin zone reduced by all of the symmetries in the point group of the lattice.

The concept of a Brillouin zone was developed by Léon Brillouin (1889–1969), a French physicist.

Triclinic lattice system TRI(4)

Triclinic Lattice type 1a (TRI1a) BZ.
Triclinic Lattice type 1b (TRI1b) BZ.
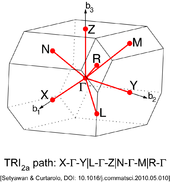Triclinic Lattice type 2a (TRI2a) BZ.
Triclinic Lattice type 2b (TRI2b) BZ.

See below for the aflowlib.org standard.

Monoclinic lattice system MCL(1), MCLC(5)

Monoclinic Lattice (MCL) BZ.
Base Centered Monoclinic Lattice type 1 (MCLC1) BZ.
Base Centered Monoclinic Lattice type 3 (MCLC3) BZ.
Base Centered Monoclinic Lattice type 4 (MCLC4) BZ.
Base Centered Monoclinic Lattice type 5 (MCLC5) BZ.

See below for the aflowlib.org standard.

Orthorhombic lattice system ORC(1), ORCC(1), ORCI(1), ORCF(3)

Simple Orthorhombic Lattice (ORC) BZ.
Base Centered Orthorhombic Lattice (ORCC) BZ.
Body Centered Orthorhombic Lattice (ORCI) BZ.
Face Centered Orthorhombic Lattice type 1 (ORCF1) BZ.
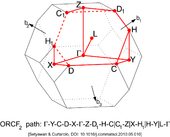Face Centered Orthorhombic Lattice type 2 (ORCF2) BZ.
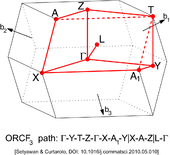Face Centered Orthorhombic Lattice type 3 (ORCF3) BZ.

See below for the aflowlib.org standard.

Tetragonal lattice system TET(1), BCT(2)

Simple Tetragonal Lattice (TET) BZ.
Body Centered Tetragonal Lattice type 1 (BCT1) BZ.
Body Centered Tetragonal Lattice type 2 (BCT2) BZ.

See below for the aflowlib.org standard.

Rhombohedral lattice system RHL(2)

Rhombohedral Lattice type 1 (RHL1) BZ.
Rhombohedral Lattice type 2 (RHL2) BZ.

See below for the aflowlib.org standard.

Hexagonal lattice system HEX(1)

Hexagonal Lattice (HEX) BZ.

See below for the aflowlib.org standard.

Cubic lattice system CUB(1),FCC(1), BCC(1)

Simple Cubic Lattice (CUB) BZ.
Body Centered Cubic Lattice (BCC) BZ.
Face Centered Cubic Lattice (FCC) BZ.

See below for the aflowlib.org standard.

See also

Brillouin-zone construction by 300keV electrons.

References

    External links

    This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.