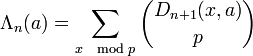Brewer sum
From Wikipedia, the free encyclopedia
In mathematics, Brewer sums are finite character sum introduced by Brewer (1961, 1966) related to Jacobsthal sums.
Definition
The Brewer sum is given by
where Dn is the Dickson polynomial (or "Brewer polynomial") given by
and () is the Legendre symbol.
The Brewer sum is zero when n is coprime to q2−1.
References
- Brewer, B. W. (1961), "On certain character sums", Transactions of the American Mathematical Society 99: 241–245, ISSN 0002-9947, MR 0120202, Zbl 0103.03205
- Brewer, B. W. (1966), "On primes of the form u²+5v²", Proceedings of the American Mathematical Society 17: 502–509, ISSN 0002-9939, MR 0188171, Zbl 0147.29801
- Berndt, Bruce C.; Evans, Ronald J. (1979), "Sums of Gauss, Eisenstein, Jacobi, Jacobsthal, and Brewer", Illinois Journal of Mathematics 23 (3): 374–437, ISSN 0019-2082, MR 537798, Zbl 0393.12029
- Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields, Encyclopedia of Mathematics and Its Applications 20 (2nd ed.), Cambridge University Press, ISBN 0-521-39231-4, Zbl 0866.11069
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.