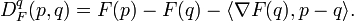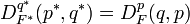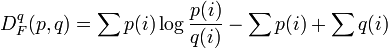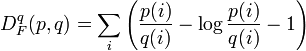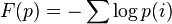Bregman divergence

From Wikipedia, the free encyclopedia

In mathematics, a Bregman divergence or Bregman distance is similar to a metric, but does not satisfy the triangle inequality nor symmetry. There are two ways in which Bregman divergences are important. Firstly, they generalize squared Euclidean distance to a class of distances that all share similar properties. Secondly, they bear a strong connection to exponential families of distributions; as has been shown by (Banerjee et al. 2005), there is a bijection between regular exponential families and regular Bregman divergences.

Bregman divergences are named after L. M. Bregman, who introduced the concept in 1967. More recently researchers in geometric algorithms have shown that many important algorithms can be generalized from Euclidean metrics to distances defined by Bregman divergence (Banerjee et al. 2005; Nielsen and Nock 2006; Boissonnat et al. 2010).

Definition

Let 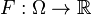$F:\Omega \to {\mathbb {R}}$ be a continuously-differentiable real-valued and strictly convex function defined on a closed convex set $\Omega$ .

The Bregman distance associated with F for points 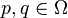$p,q\in \Omega$ is the difference between the value of F at point p and the value of the first-order Taylor expansion of F around point q evaluated at point p:

$D_{F}^{q}(p,q)=F(p)-F(q)-\langle \nabla F(q),p-q\rangle .$

Properties

Non-negativity: 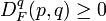$D_{F}^{q}(p,q)\geq 0$ for all p, q. This is a consequence of the convexity of F.
Convexity: 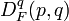$D_{F}^{q}(p,q)$ is convex in its first argument, but not necessarily in the second argument (see ^[1])
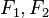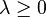Linearity: If we think of the Bregman distance as an operator on the function F, then it is linear with respect to non-negative coefficients. In other words, for $F_{1},F_{2}$ strictly convex and differentiable, and $\lambda \geq 0$ ,

$D_{{F_{1}+\lambda F_{2}}}^{q}(p,q)=D_{{F_{1}}}^{q}(p,q)+\lambda D_{{F_{2}}}^{q}(p,q)$

Duality: The function F has a convex conjugate 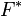$F^{*}$ . The Bregman distance defined with respect to 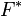$F^{*}$ has an interesting relationship to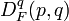 $D_{F}^{q}(p,q)$

$D_{{F^{*}}}^{{q^{*}}}(p^{*},q^{*})=D_{F}^{p}(q,p)$

Here, $p^{*}=\nabla F(p)$ is the dual point corresponding to p

A key result about Bregman divergences is that, given a random vector, the mean vector minimizes the expected Bregman divergence from the random vector. This result generalizes the textbook result that the mean of a set minimizes total squared error to elements in the set. This result was proved for the vector case by (Banerjee et al. 2005), and extended to the case of functions/distributions by (Frigyik et al. 2008). This result is important because it further justifies using a mean as a representative of a random set, particularly in Bayesian estimation.

Examples

Squared Euclidean distance $D_{F}^{y}(x,y)=\|x-y\|^{2}$ is the canonical example of a Bregman distance, generated by the convex function $F(x)=\|x\|^{2}$

The squared Mahalanobis distance, 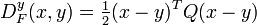$D_{F}^{y}(x,y)={\tfrac {1}{2}}(x-y)^{T}Q(x-y)$ which is generated by the convex function 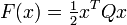$F(x)={\tfrac {1}{2}}x^{T}Qx$ . This can be thought of as a generalization of the above squared Euclidean distance.

The generalized Kullback–Leibler divergence

$D_{F}^{q}(p,q)=\sum p(i)\log {\frac {p(i)}{q(i)}}-\sum p(i)+\sum q(i)$

is generated by the convex function

$F(p)=\sum _{i}p(i)\log p(i)-\sum p(i)$

The Itakura–Saito distance,

$D_{F}^{q}(p,q)=\sum _{i}\left({\frac {p(i)}{q(i)}}-\log {\frac {p(i)}{q(i)}}-1\right)$

is generated by the convex function

$F(p)=-\sum \log p(i)$

Generalizing projective duality

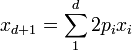A key tool in computational geometry is the idea of projective duality, which maps points to hyperplanes and vice versa, while preserving incidence and above-below relationships. There are numerous analytical forms of the projective dual: one common form maps the point $p=(p_{1},\ldots p_{d})$ to the hyperplane $x_{{d+1}}=\sum _{1}^{d}2p_{i}x_{i}$ . This mapping can be interpreted (identifying the hyperplane with its normal) as the convex conjugate mapping that takes the point p to its dual point $p^{*}=\nabla F(p)$ , where F defines the d-dimensional paraboloid $x_{{d+1}}=\sum x_{i}^{2}$ .

If we now replace the paraboloid by an arbitrary convex function, we obtain a different dual mapping that retains the incidence and above-below properties of the standard projective dual. This implies that natural dual concepts in computational geometry like Voronoi diagrams and Delaunay triangulations retain their meaning in distance spaces defined by an arbitrary Bregman divergence. Thus, algorithms from "normal" geometry extend directly to these spaces (Boissonnat, Nielsen and Nock, 2010)

Matrix Bregman divergences, functional Bregman divergences and the submodular Bregman divergences

Bregman divergences can also be defined between matrices, between functions, and between measures (distributions). Bregman divergences between matrices include the Stein's loss and von Neumann entropy. Bregman divergences between functions include total squared error, relative entropy, and squared bias; see the references by Frigyik et al. below for definitions and properties. Similarly Bregman divergences have also been defined over sets, through a submodular set function which is known as the discrete analog of a convex function. The submodular Bregman divergences subsume a number of discrete distance measures, like the Hamming distance, precision and recall, mutual information and some other set based distance measures (see Iyer & Bilmes, 2012) for more details and properties of the submodular Bregman.)

For a list of common matrix Bregman divergences, see Table 15.1 in.^[2]

References

↑ "Joint and separate convexity of the Bregman Distance", by H. Bauschke and J. Borwein, in D. Butnariu, Y. Censor, and S. Reich, editors, Inherently Parallel Algorithms in Feasibility and Optimization and their Applications, Elsevier 2001
↑ "Matrix Information Geometry", R. Nock, B. Magdalou, E. Briys and F. Nielsen, pdf, from this book

Banerjee, Arindam; Merugu, Srujana; Dhillon, Inderjit S.; Ghosh, Joydeep (2005). "Clustering with Bregman divergences". Journal of Machine Learning Research 6: 1705–1749.
Bregman, L. M. (1967). "The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming". USSR Computational Mathematics and Mathematical Physics 7 (3): 200–217. doi:10.1016/0041-5553(67)90040-7.
Frigyik, Bela A.; Srivastava, Santosh; Gupta, Maya R. (2008). "Functional Bregman Divergences and Bayesian Estimation of Distributions". IEEE Transactions on Information Theory 54 (11): 5130–5139. doi:10.1109/TIT.2008.929943.
Iyer, Rishabh.; Bilmes, Jeff (2012). "The Submodular Bregman divergences and Lovasz Bregman divergences with Applications". Conference on Neural Information Processing Systems.
Frigyik, Bela A.; Srivastava, Santosh; Gupta, Maya R. (2008). An Introduction to Functional Derivatives. UWEE Tech Report 2008-0001. University of Washington, Dept. of Electrical Engineering.
Nielsen, Frank; Nock, Richard (2009). "The dual Voronoi diagrams with respect to representational Bregman divergences". Proc. 6th International Symposium on Voronoi Diagrams. IEEE. doi:10.1109/ISVD.2009.15.
Nielsen, Frank; Nock, Richard (2007). "On the Centroids of Symmetrized Bregman Divergences". arXiv:0711.3242 [cs.CG].
Nielsen, Frank; Boissonnat, Jean-Daniel; Nock, Richard (2007). "On Visualizing Bregman Voronoi diagrams". Proc. 23rd ACM Symposium on Computational Geometry (video track).
Boissonnat, Jean-Daniel; Nielsen, Frank; Nock, Richard (2010). "Bregman Voronoi Diagrams". Discrete and Computational Geometry. 44 (2).
Nielsen, Frank; Nock, Richard (2006). "On approximating the smallest enclosing Bregman Balls". Proc. 22nd ACM Symposium on Computational Geometry. pp. 485–486. doi:10.1145/1137856.1137931.

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.