Brauner space
From Wikipedia, the free encyclopedia
In functional analysis and related areas of mathematics Brauner space is a complete compactly generated locally convex space  having a sequence of compact sets
having a sequence of compact sets 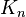 such that every other compact set
such that every other compact set 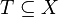 is contained in some
is contained in some 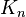 .
.
Brauner spaces are named after Kalman Brauner,[1] who first started to study them. All Brauner spaces are stereotype and are in the stereotype duality relations with Fréchet spaces:[2][3]
- for any Fréchet space
 its stereotype dual space[4]
its stereotype dual space[4]  is a Brauner space,
is a Brauner space, - and vice versa, for any Brauner space
 its stereotype dual space
its stereotype dual space  is a Fréchet space.
is a Fréchet space.
- for any Fréchet space
Examples
- Let
 be a
be a 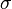 -compact locally compact topological space, and
-compact locally compact topological space, and 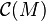 the space of all functions on
the space of all functions on  (with values in
(with values in 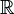 or
or 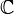 ), endowed with the usual topology of uniform convergence on compact sets in
), endowed with the usual topology of uniform convergence on compact sets in  . The dual space
. The dual space 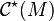 of measures with compact support in
of measures with compact support in  with the topology of uniform convergence on compact sets in
with the topology of uniform convergence on compact sets in 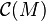 is a Brauner space.
is a Brauner space.
- Let
 be a smooth manifold, and
be a smooth manifold, and 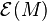 the space of smooth functions on
the space of smooth functions on  (with values in
(with values in 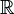 or
or 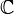 ), endowed with the usual topology of uniform convergence with each derivative on compact sets in
), endowed with the usual topology of uniform convergence with each derivative on compact sets in  . The dual space
. The dual space 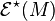 of distributions with compact support in
of distributions with compact support in  with the topology of uniform convergence on bounded sets in
with the topology of uniform convergence on bounded sets in 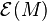 is a Brauner space.
is a Brauner space.
- Let
 be a Stein manifold and
be a Stein manifold and 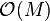 the space of holomorphic functions on
the space of holomorphic functions on  with the usual topology of uniform convergence on compact sets in
with the usual topology of uniform convergence on compact sets in  . The dual space
. The dual space  of analytic functionals on
of analytic functionals on  with the topology of uniform convergence on biunded sets in
with the topology of uniform convergence on biunded sets in 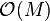 is a Brauner space.
is a Brauner space.
- Let
 be a compactly generated Stein group. The space
be a compactly generated Stein group. The space 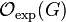 of holomorphic functions of exponential type on
of holomorphic functions of exponential type on  is a Brauner space with respect to a natural topology.[3]
is a Brauner space with respect to a natural topology.[3]
Notes
References
- Schaefer, Helmuth H. (1966). Topological vector spaces. New York: The MacMillan Company. ISBN 0-387-98726-6.
- Robertson, A.P.; Robertson, W.J. (1964). Topological vector spaces. Cambridge Tracts in Mathematics 53. Cambridge University Press.
- Brauner, K. (1973). "Duals of Frechet spaces and a generalization of the Banach-Dieudonne theorem". Duke Math. Jour. 40 (4): 845–855. doi:10.1215/S0012-7094-73-04078-7.
- Akbarov, S.S. (2003). "Pontryagin duality in the theory of topological vector spaces and in topological algebra". Journal of Mathematical Sciences 113 (2): 179–349. doi:10.1023/A:1020929201133.
- Akbarov, S.S. (2009). "Holomorphic functions of exponential type and duality for Stein groups with algebraic connected component of identity(subscription required)". Journal of Mathematical Sciences 162 (4): 459–586. doi:10.1007/s10958-009-9646-1.
| ||||||||||||||||||||||||||
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.
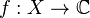 endowed with the topology of uniform convergence on totally bounded sets in
endowed with the topology of uniform convergence on totally bounded sets in