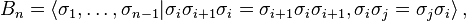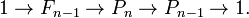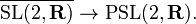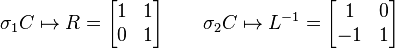Braid group

From Wikipedia, the free encyclopedia

In mathematics, the braid group on $n$ strands, denoted by $B n$ , is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group $S n$ . Here, $n$ is a natural number; if $n > 1$ , then $B n$ is an infinite group. Braid groups find applications in knot theory, since any knot may be represented as the closure of certain braids.

Introduction

Intuitive description

In this introduction let $n = 4$ ; the generalization to other values of $n$ will be straightforward. Consider two sets of four items lying on a table, with the items in each set being arranged in a vertical line, and such that one set sits next to the other. (In the illustrations below, these are the black dots.) Using four strands, each item of the first set is connected with an item of the second set so that a one-to-one correspondence results. Such a connection is called a braid. Often some strands will have to pass over or under others, and this is crucial: the following two connections are different braids:

is different from

On the other hand, two such connections which can be made to look the same by "pulling the strands" are considered the same braid:

is the same as

All strands are required to move from left to right; knots like the following are not considered braids:

is not a braid

Any two braids can be composed by drawing the first next to the second, identifying the four items in the middle, and connecting corresponding strands:

composed with

yields

Another example:

composed with

yields

The composition of the braids $σ$ and $τ$ is written as $στ$ .

The set of all braids on four strands is denoted by $B 4$ . The above composition of braids is indeed a group operation. The identity element is the braid consisting of four parallel horizontal strands, and the inverse of a braid consists of that braid which "undoes" whatever the first braid did, which is obtained by flipping a diagram such as the ones above across a vertical line going through its centre. (The first two example braids above are inverses of each other.)

Formal treatment

To put the above informal discussion of braid groups on firm ground, one needs to use the homotopy concept of algebraic topology, defining braid groups as fundamental groups of a configuration space. This is outlined in the article on braid theory.

Alternatively, one can define the braid group purely algebraically via the braid relations, keeping the pictures in mind only to guide the intuition.

History

Braid groups were introduced explicitly by Emil Artin in 1925, although (as Wilhelm Magnus pointed out in 1974^[1]) they were already implicit in Adolf Hurwitz's work on monodromy (1891). In fact, as Magnus says, Hurwitz gave the interpretation of a braid group as the fundamental group of a configuration space (cf. braid theory), an interpretation that was lost from view until it was rediscovered by Ralph Fox and Lee Neuwirth in 1962.

Basic properties

Generators and relations

Consider the following three braids:


σ₁	σ₂	σ₃

Every braid in $B 4$ can be written as a composition of a number of these braids and their inverses. In other words, these three braids generate the group $B 4$ . To see this, an arbitrary braid is scanned from left to right for crossings; beginning at the top, whenever a crossing of strands $i$ and $i + 1$ is encountered, $σ i$ or $σ i -1$ is written down, depending on whether strand $i$ moves under or over strand $i + 1$ . Upon reaching the right hand end, the braid has been written as a product of the σ's and their inverses.

It is clear that

(i)

σ 1 σ 3 = σ 3 σ 1

while the following two relations are not quite as obvious:

(iia)

σ 1 σ 2 σ 1 = σ 2 σ 1 σ 2

(iib)

σ 2 σ 3 σ 2 = σ 3 σ 2 σ 3

(these can be appreciated best by drawing the braid on a piece of paper). It can be shown that all other relations among the braids $σ 1, σ 2$ and $σ 3$ already follow from these relations and the group axioms.

Generalising this example to $n$ strands, the group $B n$ can be abstractly defined via the following presentation:

$B_{n}=\left\langle \sigma _{1},\ldots ,\sigma _{{n-1}}|\sigma _{i}\sigma _{{i+1}}\sigma _{i}=\sigma _{{i+1}}\sigma _{i}\sigma _{{i+1}},\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\right\rangle ,$

where in the first group of relations $1 \leq i \leq n -2$ and in the second group of relations, $| i - j | \geq 2$ . This presentation leads to generalisations of braid groups called Artin groups. The cubic relations, known as the braid relations, play an important role in the theory of Yang–Baxter equation.

Further properties

The braid group $B 1$ is trivial, $B 2$ is an infinite cyclic group $Z$ , and $B 3$ is isomorphic to the knot group of the trefoil knot – in particular, it is an infinite non-abelian group.

The $n$ -strand braid group $B n$ embeds as a subgroup into the $(n +1)$ -strand braid group $B n +1$ by adding an extra strand that does not cross any of the first $n$ strands. The increasing union of the braid groups with all $n \geq 1$ is the infinite braid group $B \infty$ .

All non-identity elements of $B n$ have infinite order; i.e., $B n$ is torsion-free.

There is a left-invariant linear order on $B n$ called the Dehornoy order.

For $n \geq 3$ , $B n$ contains a subgroup isomorphic to the free group on two generators.

There is a homomorphism $B n \to Z$ defined by $σ i \mapsto 1$ . So for instance, the braid $σ 2 σ 3 σ 1 -1 σ 2 σ 3$ is mapped to $1 + 1 - 1 + 1 + 1 = 3$ .

Interactions of braid groups

Relation with symmetric group and the pure braid group

By forgetting how the strands twist and cross, every braid on $n$ strands determines a permutation on $n$ elements. This assignment is onto, compatible with composition, and therefore becomes a surjective group homomorphism $B n \to S n$ from the braid group into the symmetric group. The image of the braid σ_i ∈ $B n$ is the transposition $s i = (i, i +1) \in S n$ . These transpositions generate the symmetric group, satisfy the braid group relations, and have order 2. This transforms the Artin presentation of the braid group into the Coxeter presentation of the symmetric group:

$S_{n}=\left\langle s_{1},\ldots ,s_{{n-1}}|s_{i}s_{{i+1}}s_{i}=s_{{i+1}}s_{i}s_{{i+1}},s_{i}s_{j}=s_{j}s_{i}{\text{ for }}|i-j|\geq 2,s_{i}^{2}=1\right\rangle .$

The kernel of the homomorphism $B n \to S n$ is the subgroup of $B n$ called the pure braid group on $n$ strands and denoted $P n$ . In a pure braid, the beginning and the end of each strand are in the like positions. Pure braid groups fit into a short exact sequence

$1\to F_{{n-1}}\to P_{n}\to P_{{n-1}}\to 1.$

This sequence splits and therefore pure braid groups are realized as iterated semi-direct products of free groups.

Relation between $B 3$ and the modular group

B 3

is the universal central extension of the modular group.

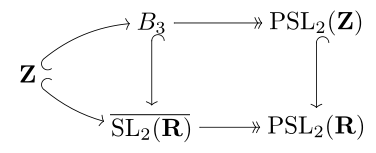
The braid group $B 3$ is the universal central extension of the modular group $PSL(2, Z)$ , with these sitting as lattices inside the (topological) universal covering group

$\overline {{\mathrm {SL}}(2,{\mathbf {R}})}\to {\mathrm {PSL}}(2,{\mathbf {R}}).$

Furthermore, the modular group has trivial center, and thus the modular group is isomorphic to the quotient group of $B 3$ modulo its center, $Z (B 3)$ , and equivalently, to the group of inner automorphisms of $B 3$ .

Here is a construction of this isomorphism. Define

$a=\sigma _{1}\sigma _{2}\sigma _{1},\quad b=\sigma _{1}\sigma _{2}.$

From the braid relations it follows that $a 2 = b 3$ . Denoting this latter product as $c$ , one may verify from the braid relations that

$\sigma _{1}c\sigma _{1}^{{-1}}=\sigma _{2}c\sigma _{2}^{{-1}}=c$

implying that $c$ is in the center of $B 3$ . Let $C$ denote the subgroupof $B 3$ generated by $c$ , since $C \subset Z (B 3)$ , it is a normal subgroup and one may take the quotient group $B 3 / C$ . We claim $B 3 / C ≅ PSL(2, Z)$ ; this isomorphism can be given an explicit form. The cosets $σ 1 C$ and $σ 2 C$ map to

$\sigma _{1}C\mapsto R={\begin{bmatrix}1&1\\0&1\end{bmatrix}}\qquad \sigma _{2}C\mapsto L^{{-1}}={\begin{bmatrix}1&0\\-1&1\end{bmatrix}}$

where $L$ and $R$ are the standard left and right moves on the Stern-Brocot tree; it is well known that these moves generate the modular group.

Alternately, one common presentation for the modular group is

$\langle v,p\,|\,v^{2}=p^{3}=1\rangle$

where

$v={\begin{bmatrix}0&1\\-1&0\end{bmatrix}},\qquad p={\begin{bmatrix}0&1\\-1&1\end{bmatrix}}.$

Mapping $a$ to $v$ and $b$ to $p$ yields a surjective group homomorphism $B 3 \to PSL(2, Z)$ .

The center of $B 3$ is equal to $C$ , a consequence of the facts that $c$ is in the center, the modular group has trivial center, and the above surjective homomorphism has kernel $C$ .

Relationship to the mapping class group and classification of braids

The braid group $B n$ can be shown to be isomorphic to the mapping class group of a punctured disk with $n$ punctures. This is most easily visualized by imagining each puncture as being connected by a string to the boundary of the disk; each mapping homeomorphism that permutes two of the punctures can then be seen to be a homotopy of the strings, that is, a braiding of these strings.

Via this mapping class group interpretation of braids, each braid may be classified as periodic, reducible or pseudo-Anosov.

Connection to knot theory

If a braid is given and one connects the first left-hand item to the first right-hand item using a new string, the second left-hand item to the second right-hand item etc. (without creating any braids in the new strings), one obtains a link, and sometimes a knot. Alexander's theorem in braid theory states that the converse is true as well: every knot and every link arises in this fashion from at least one braid; such a braid can be obtained by cutting the link. Since braids can be concretely given as words in the generators $σ i$ , this is often the preferred method of entering knots into computer programs.

Computational aspects

The word problem for the braid relations is efficiently solvable and there exists a normal form for elements of $B n$ in terms of the generators $σ 1, ..., σ n -1$ . (In essence, computing the normal form of a braid is the algebraic analogue of "pulling the strands" as illustrated in our second set of images above.) The free GAP computer algebra system can carry out computations in $B n$ if the elements are given in terms of these generators. There is also a package called CHEVIE for GAP3 with special support for braid groups. The word problem is also efficiently solved via the Lawrence-Krammer representation.

Since there are nevertheless several hard computational problems about braid groups, applications in cryptography have been suggested.

Actions of braid groups

In analogy with the action of the symmetric group by permutations, in various mathematical settings there exists a natural action the braid group on $n$ -tuples of objects or on the $n$ -folded tensor product that involves some "twists". Consider an arbitrary group $G$ and let $X$ be the set of all $n$ -tuples of elements of $G$ whose product is the identity element of $G$ . Then $B n$ acts on $X$ in the following fashion:

$\sigma _{i}\left(x_{1},\ldots ,x_{{i-1}},x_{i},x_{{i+1}},\ldots ,x_{n}\right)=\left(x_{1},\ldots ,x_{{i-1}},x_{{i+1}},x_{{i+1}}^{{-1}}x_{i}x_{{i+1}},x_{{i+2}},\ldots ,x_{n}\right).$

Thus the elements $x i$ and $x i +1$ exchange places and, in addition, $x i$ is twisted by the inner automorphism corresponding to $x i +1$ — this ensures that the product of the components of $x$ remains the identity element. It may be checked that the braid group relations are satisfied and this formula indeed defines a group action of $B n$ on $X$ . As another example, a braided monoidal category is a monoidal category with a braid group action. Such structures play an important role in modern mathematical physics and lead to quantum knot invariants.

Representations

Elements of the braid group $B n$ can be represented more concretely by matrices. One classical such representation is Burau representation, where the matrix entries are single variable Laurent polynomials. It had been a long-standing question whether Burau representation was faithful, but the answer turned out to be negative for $n \geq 5$ . More generally, it was a major open problem whether braid groups were linear. In 1990, Ruth Lawrence described a family of more general "Lawrence representations" depending on several parameters. In 1996, C. Nayak and Frank Wilczek posited that in analogy to projective representations of $SO(3)$ , the projective representations of the braid group have a physical meaning for certain quasiparticles in the fractional quantum hall effect. Around 2001 Stephen Bigelow and Daan Krammer independently proved that all braid groups are linear. Their work used the Lawrence–Krammer representation of dimension $n (n -1)/2$ depending on the variables $q$ and $t$ . By suitably specializing these variables, the braid group $B n$ may be realized as a subgroup of the general linear group over the complex numbers.

Infinitely generated braid groups

There are many ways to generalize this notion to an infinite number of strands. The simplest way is take the direct limit of braid groups, where the attaching maps $f : B n \to B n +1$ send the $n -1$ generators of $B n$ to the first $n -1$ generators of $B n +1$ (i.e., by attaching a trivial strand). Fabel has shown that there are two topologies that can be imposed on the resulting group each of whose completion yields a different group. One is a very tame group and is isomorphic to the mapping class group of the infinitely punctured disk — a discrete set of punctures limiting to the boundary of the disk.

The second group can be thought of the same as with finite braid groups. Place a strand at each of the points $(0, 1/ n)$ and the set of all braids — where a braid is defined to be a collection of paths from the points $(0, 1/ n, 0)$ to the points $(0, 1/ n, 1)$ so that the function yields a permutation on endpoints — is isomorphic to this wilder group. An interesting fact is that the pure braid group in this group is isomorphic to both the inverse limit of finite pure braid groups $P n$ and to the fundamental group of the Hilbert cube minus the set

$\{(x_{i})_{{i\in {\mathbb {N}}}}\mid x_{i}=x_{j}{\text{ for some }}i\neq j\}.$

Notes

↑ Wilhelm Magnus. Braid groups: A survey. In Lecture Notes in Mathematics, volume 372, pages 463–487. Springer, 1974. Proceedings of the Second International Conference on the Theory of Groups, Canberra, Australia, 1973. ISBN 978-3-540-06845-7

References

Deligne, Pierre (1972), "Les immeubles des groupes de tresses généralisés", Inventiones Mathematicae 17 (4): 273–302, doi:10.1007/BF01406236, ISSN 0020-9910, MR 0422673

External links

Braid group, PlanetMath.org.
CRAG: CRyptography and Groups at Algebraic Cryptography Center Contains extensive library for computations with Braid Groups
P. Fabel, Completing Artin's braid group on infinitely many strands, Journal of Knot Theory and its Ramifications, Vol. 14, No. 8 (2005) 979–991
P. Fabel, The mapping class group of a disk with infinitely many holes, Journal of Knot Theory and its Ramifications, Vol. 15, No. 1 (2006) 21–29
Chernavskii, A.V. (2001), "Braid theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Stephen Bigelow's exploration of B5 Java applet.
C. Nayak and F. Wilczek's connection of projective braid group representations to the fractional quantum Hall effect
Presentation for FradkinFest by C. V. Nayak
N. Read's criticism of the reality of Wilczek-Nayak representation
Cryptography and Braid Groups page - Helger Lipmaa
Braid group: List of Authority Articles on arxiv.org.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.