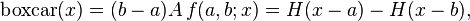Boxcar function
From Wikipedia, the free encyclopedia

A graphical representation of a boxcar function
In mathematics, a boxcar function is any function which is zero over the entire real line except for a single interval where it is equal to a constant, A; it is a simple step function.[1] The boxcar function can be expressed in terms of the uniform distribution as
where f(a,b;x) is the uniform distribution of x for the interval [a, b] and  is the Heaviside step function.
As with most such discontinuous functions, there is a question of the value at the transition points. These values are probably best chosen for each individual application.
is the Heaviside step function.
As with most such discontinuous functions, there is a question of the value at the transition points. These values are probably best chosen for each individual application.
When a boxcar function is selected as the impulse response of a filter, the result is a moving average filter.
The function is named after its resemblance to a boxcar, a type of railroad car.
See also
References
- ↑ Weisstein, Eric W. "Boxcar Function". MathWorld. Retrieved 13 September 2013.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.