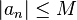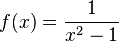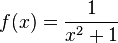Bounded function

From Wikipedia, the free encyclopedia

A schematic illustration of a bounded function (red) and an unbounded one (blue). Intuitively, the graph of a bounded function stays within a horizontal band, while the graph of an unbounded function does not.

In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M such that

$|f(x)|\leq M$

for all x in X. A function that is not bounded is said to be unbounded.

Sometimes, if f(x) ≤ A for all x in X, then the function is said to be bounded above by A. On the other hand, if f(x) ≥ B for all x in X, then the function is said to be bounded below by B.

The concept should not be confused with that of a bounded operator.

An important special case is a bounded sequence, where X is taken to be the set N of natural numbers. Thus a sequence f = (a₀, a₁, a₂, ...) is bounded if there exists a real number M such that

$|a_{n}|\leq M$

for every natural number n. The set of all bounded sequences, equipped with a vector space structure, forms a sequence space.

This definition can be extended to functions taking values in a metric space Y. Such a function f defined on some set X is called bounded if for some a in Y there exists a real number M such that its distance function d ("distance") is less than M, i.e.

$d(f(x),a)\leq M$

for all x in X.

If this is the case, there is also such an M for each other a, by the triangle inequality.

Examples

The function f : R → R defined by f(x) = sin(x) is bounded. The sine function is no longer bounded if it is defined over the set of all complex numbers.
The function

$f(x)={\frac {1}{x^{2}-1}}$

defined for all real x except for −1 and 1 is unbounded. As x gets closer to −1 or to 1, the values of this function get larger and larger in magnitude. This function can be made bounded if one considers its domain to be, for example, [2, ∞) or (−∞, −2].

The function

$f(x)={\frac {1}{x^{2}+1}}$

defined for all real x is bounded.

Every continuous function f : [0, 1] → R is bounded. This is really a special case of a more general fact: Every continuous function from a compact space into a metric space is bounded.
The function f which takes the value 0 for x rational number and 1 for x irrational number is bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on [0, 1] is much bigger than the set of continuous functions on that interval.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.