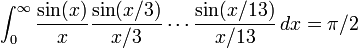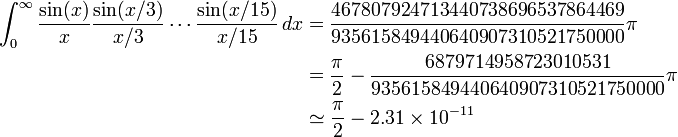Borwein integral

From Wikipedia, the free encyclopedia

In mathematics, a Borwein integral is an integral involving products of sinc(ax), where the sinc function is given by sinc(x) = sin(x)/x for x not equal to 0, and sinc(0) = 1.^[1]^[2] These integrals are notorious for exhibiting apparent patterns that eventually break down. An example is as follows:

${\begin{aligned}&\int _{0}^{\infty }{\frac {\sin(x)}{x}}\,dx=\pi /2\\[10pt]&\int _{0}^{\infty }{\frac {\sin(x)}{x}}{\frac {\sin(x/3)}{x/3}}\,dx=\pi /2\\[10pt]&\int _{0}^{\infty }{\frac {\sin(x)}{x}}{\frac {\sin(x/3)}{x/3}}{\frac {\sin(x/5)}{x/5}}\,dx=\pi /2\end{aligned}}$

This pattern continues up to

$\int _{0}^{\infty }{\frac {\sin(x)}{x}}{\frac {\sin(x/3)}{x/3}}\cdots {\frac {\sin(x/13)}{x/13}}\,dx=\pi /2$

However at the next step the obvious pattern fails:

${\begin{aligned}\int _{0}^{\infty }{\frac {\sin(x)}{x}}{\frac {\sin(x/3)}{x/3}}\cdots {\frac {\sin(x/15)}{x/15}}\,dx&={\frac {467807924713440738696537864469}{935615849440640907310521750000}}\pi \\&={\frac {\pi }{2}}-{\frac {6879714958723010531}{935615849440640907310521750000}}\pi \\&\simeq {\frac {\pi }{2}}-2.31\times 10^{{-11}}\end{aligned}}$

In general similar integrals have value π/2 whenever the numbers 3, 5, ... are replaced by positive real numbers such that the sum of their reciprocals is less than 1. In the example above, 1/3 + 1/5 + ... + 1/13 < 1, but 1/3 + 1/5 + ... + 1/15 > 1.

References

↑ Borwein, David; Borwein, Jonathan M. (2001), "Some remarkable properties of sinc and related integrals", The Ramanujan Journal 5 (1): 73–89, doi:10.1023/A:1011497229317, ISSN 1382-4090, MR 1829810
↑ Baillie, Robert (2011). "Fun With Very Large Numbers". arXiv:1105.3943v1 [math.NT].

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.