Born–Haber cycle
The Born–Haber cycle is an approach to analyze reaction energies. It was named after and developed by the two German scientists Max Born and Fritz Haber. The cycle is concerned with the formation of an ionic compound from the reaction of a metal (often a Group I or Group II element) with a halogen.
Born–Haber cycles are used primarily as a means of calculating lattice energies (or more precisely enthalpies[note 1]) which cannot otherwise be measured directly. The lattice enthalpy is the enthalpy change involved in the formation of an ionic compound from gaseous ions. Some chemists define it as the energy to break the ionic compound into gaseous ions. The former definition is invariably exothermic and the latter is endothermic. A Born–Haber cycle applies Hess' Law to calculate the lattice enthalpy by comparing the standard enthalpy change of formation of the ionic compound (from the elements) to the enthalpy required to make gaseous ions from the elements.
This latter calculation is complex. To make gaseous ions from elements it is necessary to atomise the elements (turn each into gaseous atoms) and then to ionise the atoms. If the element is normally a molecule then we first have to consider its bond dissociation enthalpy (see also bond energy). The energy required to remove one or more electrons to make a cation is a sum of successive ionization energies; for example the energy needed to form Mg2+ is the first plus the second ionization energies of Mg. The energy changes when successive electrons are added to an atom to make it an anion are called the electron affinities.
The Born–Haber cycle applies only to fully ionic solids such as certain alkali halides. Most compounds include covalent and ionic contributions to chemical bonding and to the lattice energy, which is represented by an extended Born-Haber thermodynamic cycle.[1] The extended Born–Haber cycle can be used to estimate the polarity and the atomic charges of polar compounds.
Example: Formation of lithium fluoride

The enthalpy of formation of lithium fluoride (LiF) from its elements lithium and fluorine in their stable forms is modeled in five steps in the diagram:
- Enthalpy change of atomization enthalpy of lithium
- Ionization enthalpy of lithium
- Atomization enthalpy of fluorine
- Electron affinity of fluorine
- Lattice enthalpy
The same calculation applies for any metal other than lithium or any non-metal other than fluorine.
The sum of the energies for each step of the process must equal the enthalpy of formation of the metal and non-metal, 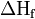 .
.
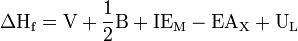
- V is the enthalpy of sublimation for metal atoms (lithium)
- B is the bond energy (of F2). The coefficient 1/2 is used because the formation reaction is Li + 1/2 F2 → LiF.
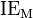 is the ionization energy of the metal atom:
is the ionization energy of the metal atom: 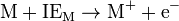
 is the electron affinity of non-metal atom X (fluorine)
is the electron affinity of non-metal atom X (fluorine)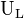 is the lattice energy (defined as exothermic here)
is the lattice energy (defined as exothermic here)
The net enthalpy of formation and the first four of the five energies can be determined experimentally, but the lattice energy cannot be measured directly. Instead, the lattice energy is calculated by subtracting the other four energies in the Born–Haber cycle from the net enthalpy of formation.[2]
The word cycle refers to the fact that one can also equate to zero the total enthalpy change for a cyclic process, starting and ending with LiF(s) in the example. This leads to
 which is equivalent to the previous equation.
which is equivalent to the previous equation.
See also
Notes
- ↑ The difference between energy and enthalpy is very small and the two terms are interchanged freely in this article.
References
- ↑ H. Heinz and U. W. Suter Journal of Physical Chemistry B 2004, 108, 18341-18352.
- ↑ Moore, Stanitski, and Jurs. Chemistry: The Molecular Science. 3rd edition. 2008. ISBN 0-495-10521-X. pages 320-321.