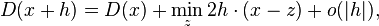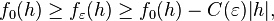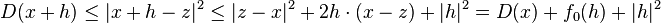Bony–Brezis theorem

From Wikipedia, the free encyclopedia

In mathematics, the Bony–Brezis theorem, due to the French mathematicians Jean-Michel Bony and Haïm Brezis, gives necessary and sufficient conditions for a closed subset of a manifold to be invariant under the flow defined by a vector field, namely at each point of the closed set the vector field must have non-positive inner product with any exterior normal vector to the set. A vector is an exterior normal at a point of the closed set if there is a real-valued continuously differentiable function maximized locally at the point with that vector as its derivative at the point. If the closed subset is a smooth submanifold with boundary, the condition states that the vector field should not point outside the subset at boundary points. The generalization to non-smooth subsets is important in the theory of partial differential equations.

Statement

Let F be closed subset of a C² manifold M and let X be a vector field on M which is Lipschitz continuous. The following conditions are equivalent:

Any integral curve of X starting in F remains in F.
(X(m),v) ≤ 0 for any exterior normal vector v at a point m in F.

Proof

Following Hörmander (1983), to prove that the first condition implies the second, let c(t) be an integral curve with c(0) = x in F and dc/dt= X(c). Let g have a local maximum on F at x. Then g(c(t)) ≤ g (c(0)) for t small and positive. Differentiating, this implies that g '(x)⋅X(x) ≤ 0.

To prove the reverse implication, since the result is local. it enough to check it in Rⁿ. In that case X locally satisfies a Lipschitz condition

$\displaystyle {|X(a)-X(b)|\leq C|a-b|.}$

If F is closed, the distance function D(x) = d(x,F)² has the following differentiability property:

$\displaystyle {D(x+h)=D(x)+\min _{{z}}2h\cdot (x-z)+o(|h|),}$

where the minimum is taken over the closest points z to x in F.

To check this, let

$\displaystyle {f_{\varepsilon }(h)=\min _{{z}}2h\cdot (x-z),}$

where the minimum is taken over z in F such that d(x,z) ≤ d(x,F) + ε.

Since f_ε is homogeneous in h and increases uniformly to f₀ on any sphere,

$\displaystyle {f_{0}(h)\geq f_{\varepsilon }(h)\geq f_{0}(h)-C(\varepsilon )|h|,}$

with a constant C(ε) tending to 0 as ε tends to 0.

This differentiability property follows from this because

$\displaystyle {D(x+h)\leq |x+h-z|^{2}\leq |z-x|^{2}+2h\cdot (x-z)+|h|^{2}=D(x)+f_{0}(h)+|h|^{2}}$

and similarly if |h| ≤ ε

$\displaystyle {D(x+h)\geq D(x)+f_{\varepsilon }(h)+|h|^{2}.}$

The differentiability property implies that

$\displaystyle {\lim {\delta \downarrow 0}{D(c(t+\delta ))-D(c(t)) \over \delta }=2\min _{z}X(c(t))\cdot (c(t)-z),}$

minimized over closest points z to c(t). For any such z

$\displaystyle {2X(c(t))\cdot (c(t)-z)=2X(z)\cdot (c(t)-z)-2(X(z)-X(c(t)))\cdot (c(t)-z).}$

Since −|y − c(t)|² has a local maximum on F at y = z, c(t) − z is an exterior normal vector at z. So the first term on the right hand side is non-negative. The Lipschitz condition for X implies the second term is bounded above by 2C⋅D(c(t)). Thus the derivative from the right of

$\displaystyle {e^{{-2Ct}}D(c(t))}$

is non-positive, so it is a non-increasing function of t. Thus if c(0) lies in F, D(c(0))=0 and hence D(c(t)) = 0 for t > 0, i.e. c(t) lies in F for t > 0.

References

Bony, Jean-Michel (1969), "Principe du Maximum, inégalité de Harnack et unicité du problème de Cauchy pour les opérateurs elliptiques dégénerés", Ann. Inst. Fourier 19: 277–304
Brezis, Haim (1970), "On a characterization of flow-invariant sets", Comm. Pure App. Math. 223: 261–263
Hörmander, Lars (1983), Analysis of Partial Differential Operators I, Springer-Verlag, pp. 300–305, ISBN 3-540-12104-8 , Theorem 8.5.11
Redheffer, R. M. (1972), "The Theorems of Bony and Brezis on Flow-Invariant Sets", The American Mathematical Monthly 79: 740–747

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.