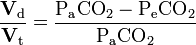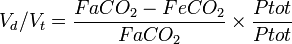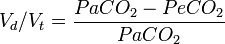Bohr equation

From Wikipedia, the free encyclopedia

The Bohr equation, named after Danish physician Christian Bohr (1855–1911), describes the amount of physiological dead space in a person's lungs. This is given as a ratio of dead space to tidal volume. It differs from anatomical dead space as measured by Fowler's method as it includes alveolar dead space.

Description

The Bohr equation is used to quantify the ratio of physiological dead space to the total tidal volume, and gives an indication of the extent of wasted ventilation. It is stated as follows:^[1]

${\frac {{\mathbf {V}}_{{{\mathrm {d}}}}}{{\mathbf {V}}_{{{\mathrm {t}}}}}}={\frac {{{\mathrm {P}}_{{{\mathrm {a}}}}{{\mathrm {CO}}}_{{{\mathrm {2}}}}}-{{\mathrm {P}}_{{{\mathrm {e}}}}{{\mathrm {CO}}}_{{{\mathrm {2}}}}}}{{\mathrm {P}}_{{{\mathrm {a}}}}{{\mathrm {CO}}}_{{{\mathrm {2}}}}}}$

Derivation

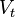Its derivation is based on the fact that only the ventilated gases involved in gas exchange ( $V_{a}$ ) will produce CO₂. Because the Total tidal volume ( $V_{t}$ ) is made up of 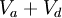$V_{a}+V_{d}$ (alveolar volume + dead space volume), we can substitute $V_{a}$ for $V_{t}-V_{d}$ .

Initially, Bohr tells us Vt = Vd + Va. The Bohr equation helps us find the amount of any expired gas, CO₂, N₂, O₂, etc. In this case we will focus on CO₂. Defining Fe as the fraction of expired CO₂ and Fa as the fraction of expired alveolar CO₂, and Fd as fraction of expired dead space volume CO₂, we can say
Vt x Fe = ( Vd x Fd ) + (Va x Fa ). This merely means all the CO₂ expired comes from two parts, the dead space volume and the alveolar volume.
If we suppose that Fd = 0 (since carbon dioxide concentration in air is normally negligible), then we can say that:^[2]

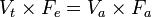$V_{t}\times F_{e}=V_{a}\times F_{a}$ Where F_e = Fraction expired CO₂, and Fa = Alveolar fraction of CO₂.

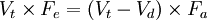$V_{t}\times F_{e}=(V_{t}-V_{d})\times F_{a}$ Substituted as above.

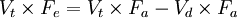$V_{t}\times F_{e}=V_{t}\times F_{a}-V_{d}\times F_{a}$ Multiply out of the brackets.

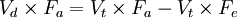$V_{d}\times F_{a}=V_{t}\times F_{a}-V_{t}\times F_{e}$ Rearrange.

$V_{d}\times F_{a}=V_{t}\times (F_{a}-F_{e})$

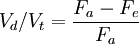$V_{d}/V_{t}={\frac {F_{a}-F_{e}}{F_{a}}}$ Divide by V_t and by F_a.

The above equation makes sense because it describes the total CO₂ being measured by the spirometer. The only source of the CO₂ we are assuming to measure is from the alveolar space where CO₂ and O₂ exchange takes place. Thus alveolar's fractional component, F_a, will always be higher than the total CO₂ content of the expired air, F_e, thus we will be always yielding a positive number.

Where Ptot is the total pressure, we obtain:

$F_{a}\times Ptot=PaCO_{2}$ and
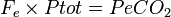
$F_{e}\times Ptot=PeCO_{2}$

Therefore:

$V_{d}/V_{t}={\frac {FaCO_{2}-FeCO_{2}}{FaCO_{2}}}\times {\frac {Ptot}{Ptot}}$

This is simplified as:

$V_{d}/V_{t}={\frac {PaCO_{2}-PeCO_{2}}{PaCO_{2}}}$

References

↑ Respiratory Physiology: The Essentials, J. West, 2005, 7th ed, Page 169
↑ Davies, Andrew, and Carl Moores. The Respiratory System. Systems of the body. Edinburgh: Churchill Livingstone, 2003.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.