Boas–Buck polynomials

From Wikipedia, the free encyclopedia

In mathematics, Boas–Buck polynomials are sequences of polynomials Φ(r)
n(x) given by generating functions of the form

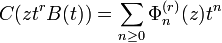$\displaystyle C(zt^{r}B(t))=\sum _{{n\geq 0}}\Phi _{n}^{{(r)}}(z)t^{n}$ .

The case r=1, sometimes called generalized Appell polynomials, was studied by Boas and Buck (1958).

References

Boas, Ralph P.; Buck, R. Creighton (1958), Polynomial expansions of analytic functions, Ergebnisse der Mathematik und ihrer Grenzgebiete. Neue Folge. 19, Berlin, New York: Springer-Verlag, MR 0094466

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.