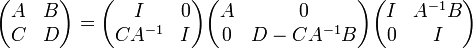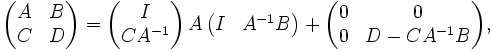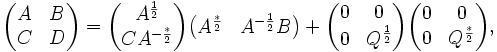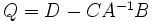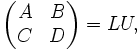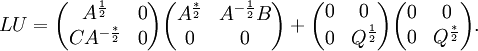Block LU decomposition

From Wikipedia, the free encyclopedia

In linear algebra, a Block LU decomposition is a matrix decomposition of a block matrix into a lower block triangular matrix L and an upper block triangular matrix U. This decomposition is used in numerical analysis to reduce the complexity of the block matrix formula.

Block LU decomposition

{\begin{pmatrix}A&B\\C&D\end{pmatrix}}={\begin{pmatrix}I&0\\CA^{{-1}}&I\end{pmatrix}}{\begin{pmatrix}A&0\\0&D-CA^{{-1}}B\end{pmatrix}}{\begin{pmatrix}I&A^{{-1}}B\\0&I\end{pmatrix}}

Block Cholesky decomposition

Consider a block matrix:

{\begin{pmatrix}A&B\\C&D\end{pmatrix}}={\begin{pmatrix}I\\CA^{{-1}}\end{pmatrix}}\,A\,{\begin{pmatrix}I&A^{{-1}}B\end{pmatrix}}+{\begin{pmatrix}0&0\\0&D-CA^{{-1}}B\end{pmatrix}},

where the matrix 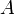{\begin{matrix}A\end{matrix}} is assumed to be non-singular, 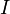{\begin{matrix}I\end{matrix}} is an identity matrix with proper dimension, and {\begin{matrix}0\end{matrix}} is a matrix whose elements are all zero.

We can also rewrite the above equation using the half matrices:

{\begin{pmatrix}A&B\\C&D\end{pmatrix}}={\begin{pmatrix}A^{{{\frac {1}{2}}}}\\CA^{{-{\frac {*}{2}}}}\end{pmatrix}}{\begin{pmatrix}A^{{{\frac {*}{2}}}}&A^{{-{\frac {1}{2}}}}B\end{pmatrix}}+{\begin{pmatrix}0&0\\0&Q^{{{\frac {1}{2}}}}\end{pmatrix}}{\begin{pmatrix}0&0\\0&Q^{{{\frac {*}{2}}}}\end{pmatrix}},

where the Schur complement of 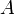{\begin{matrix}A\end{matrix}} in the block matrix is defined by

{\begin{matrix}Q=D-CA^{{-1}}B\end{matrix}}

and the half matrices can be calculated by means of Cholesky decomposition or LDL decomposition. The half matrices satisfy that

{\begin{matrix}A^{{{\frac {1}{2}}}}\,A^{{{\frac {*}{2}}}}=A;\end{matrix}}\qquad {\begin{matrix}A^{{{\frac {1}{2}}}}\,A^{{-{\frac {1}{2}}}}=I;\end{matrix}}\qquad {\begin{matrix}A^{{-{\frac {*}{2}}}}\,A^{{{\frac {*}{2}}}}=I;\end{matrix}}\qquad {\begin{matrix}Q^{{{\frac {1}{2}}}}\,Q^{{{\frac {*}{2}}}}=Q.\end{matrix}}

Thus, we have

{\begin{pmatrix}A&B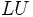\\C&D\end{pmatrix}}=LU,

where

LU={\begin{pmatrix}A^{{{\frac {1}{2}}}}&0\\CA^{{-{\frac {*}{2}}}}&0\end{pmatrix}}{\begin{pmatrix}A^{{{\frac {*}{2}}}}&A^{{-{\frac {1}{2}}}}B\\0&0\end{pmatrix}}+{\begin{pmatrix}0&0\\0&Q^{{{\frac {1}{2}}}}\end{pmatrix}}{\begin{pmatrix}0&0\\0&Q^{{{\frac {*}{2}}}}\end{pmatrix}}.

The matrix {\begin{matrix}LU\end{matrix}} can be decomposed in an algebraic manner into

L={\begin{pmatrix}A^{{{\frac {1}{2}}}}&0\\CA^{{-{\frac {*}{2}}}}&Q^{{{\frac {1}{2}}}}\end{pmatrix}}{\mathrm {~~and~~}}U={\begin{pmatrix}A^{{{\frac {*}{2}}}}&A^{{-{\frac {1}{2}}}}B\\0&Q^{{{\frac {*}{2}}}}\end{pmatrix}}.

See also

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.