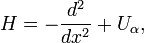Bloch spectrum

From Wikipedia, the free encyclopedia

The Bloch spectrum is a concept in quantum mechanics in the field of theoretical physics; this concept addresses certain energy spectra considerations. Let H be the one-dimensional Schrödinger equation operator

$H=-{\frac {d^{2}}{dx^{2}}}+U_{\alpha },$

where U_α is a periodic function of period α. The Bloch spectrum^[1] of H is defined as the set of values E for which all the solutions of (H − E)φ = 0 are bounded on the whole real axis. The Bloch spectrum consists of the half-line E₀ < E from which certain closed intervals [E_2j−1, E_2j] (j = 1, 2, ...) are omitted. These are forbidden bands (or gaps) so the (E_2j−2, E_2j−1) are allowed bands.

References

↑ "An upper bound on the allowed bands of the Bloch spectrum of one-dimensional Schrödinger operators with periodic potentials", N. N. Meiman, Journal of Mathematical Physics, March, 1983, volume 24, issue 3, pp. 539–540

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.