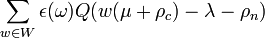Blattner's conjecture

From Wikipedia, the free encyclopedia

In mathematics, Blattner's conjecture or Blattner's formula is a description of the discrete series representations of a general semisimple group G in terms of their restricted representations to a maximal compact subgroup K (their so-called K-types). Harish-Chandra orally attributed the conjecture to Robert J Blattner, who did not publish it. It first appeared in print in Schmid (1968, theorem 2), though Okamoto & Ozeki (1967) mentioned a special case of it slightly earlier. Schmid (1972) proved Blattner's formula in some special cases, Schmid (1975a) showed that Blattner's formula gave an upper bound for the multiplicities of K-representations, Schmid (1975b) proved Blattner's conjecture for groups whose symmetric space is Hermitian, and Hecht & Schmid (1975) proved Blattner's conjecture for linear semisimple groups.

Statement

Blattner's formula says that if a discrete series representation with infinitesimal character λ is restricted to a maximal compact subgroup K, then the representation of K with highest weight μ occurs with multiplicity

$\sum _{{w\in W}}\epsilon (\omega )Q(w(\mu +\rho _{c})-\lambda -\rho _{n})$

where

Q is the number of ways a vector can be written as a sum of non-compact positive roots

W is the Weyl group

ρ_c is half the sum of the compact roots

ρ_n is half the sum of the non-compact roots

ε is the sign character of W.

Blattner's formula is what one gets by formally restricting the Harish-Chandra character formula for a discrete series representation to the maximal torus of a maximal compact group. The problem in proving the Blattner formula is that this only gives the character on the regular elements of the maximal torus, and one also needs to control its behavior on the singular elements. For non-discrete irreducible representations the formal restriction of Harish-Chandra's character formula need not give the decomposition under the maximal compact subgroup: for example, for the principal series representations of SL₂ the character is identically zero on the non-singular elements of the maximal compact subgroup, but the representation is not zero on this subgroup. In this case the character is a distribution on the maximal compact subgroup with support on the singular elements.

References

Hecht, Henryk; Schmid, Wilfried (1975), "A proof of Blattner's conjecture", Inventiones Mathematicae 31 (2): 129–154, doi:10.1007/BF01404112, ISSN 0020-9910, MR 0396855
Okamoto, Kiyosato; Ozeki, Hideki (1967), "On square-integrable ∂-cohomology spaces attached to hermitian symmetric spaces", Osaka Journal of Mathematics 4: 95–110, ISSN 0030-6126, MR 0229260
Schmid, Wilfried (1968), "Homogeneous complex manifolds and representations of semisimple Lie groups", Proceedings of the National Academy of Sciences of the United States of America 59: 56–59, ISSN 0027-8424, JSTOR 58599, MR 0225930
Schmid, Wilfried (1970), "On the realization of the discrete series of a semisimple Lie group.", Rice University Studies 56 (2): 99–108, ISSN 0035-4996, MR 0277668
Schmid, Wilfried (1975a), "Some properties of square-integrable representations of semisimple Lie groups", Annals of Mathematics. Second Series 102 (3): 535–564, ISSN 0003-486X, JSTOR 1971043, MR 0579165
Schmid, Wilfried (1975b), "On the characters of the discrete series. The Hermitian symmetric case", Inventiones Mathematicae 30 (1): 47–144, doi:10.1007/BF01389847, ISSN 0020-9910, MR 0396854

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.