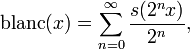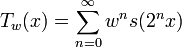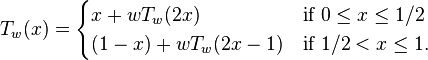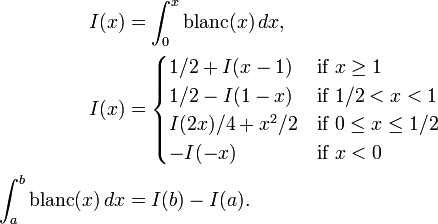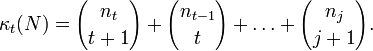Blancmange curve

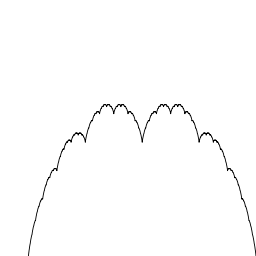
From Wikipedia, the free encyclopedia

In mathematics, the blancmange curve is a fractal curve constructible by midpoint subdivision. It is also known as the Takagi curve, after Teiji Takagi who described it in 1903, or as the Takagi–Landsberg curve, a generalization of the curve named after Takagi and Georg Landsberg. The name blancmange comes from its resemblance to a pudding of the same name. It is a special case of the more general de Rham curve.

Definition

The blancmange function is defined on the unit interval by

${{\rm {blanc}}}(x)=\sum _{{n=0}}^{\infty }{s(2^{{n}}x) \over 2^{n}},$

where $s(x)$ is defined by $s(x)=\min _{{n\in {{\mathbf Z}}}}|x-n|$ , that is, $s(x)$ is the distance from x to the nearest integer.

The Takagi–Landsberg curve is a slight generalization, given by

$T_{w}(x)=\sum _{{n=0}}^{\infty }w^{n}s(2^{{n}}x)$

for a parameter w; thus the blancmange curve is the case 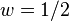$w=1/2$ . The value $H=-\log _{2}w$ is known as the Hurst parameter.

The function can be extended to all of the real line: applying the definition given above shows that the function repeats on each unit interval.

Properties

Convergence and continuity

The infinite sum defining 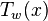$T_{w}(x)$ converges absolutely for all x: since 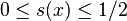$0\leq s(x)\leq 1/2$ for all 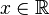$x\in {\mathbb {R}}$ , we have:

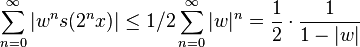$\sum _{{n=0}}^{\infty }|w^{n}s(2^{n}x)|\leq 1/2\sum _{{n=0}}^{\infty }|w|^{n}={\frac {1}{2}}\cdot {\frac {1}{1-|w|}}$ if $|w|<1$ .

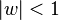Therefore, the Takagi curve of parameter w is defined on the unit interval (or 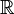${\mathbb {R}}$ ) if $|w|<1$ .

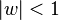The Takagi function of parameter w is continuous. Indeed, the functions 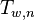$T_{{w,n}}$ defined by the partial sums 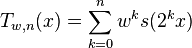$T_{{w,n}}(x)=\sum _{{k=0}}^{n}w^{k}s(2^{k}x)$ are continuous and converge uniformly toward $T_{w}$ , since:

$\left|T_{w}(x)-T_{{w,n}}(x)\right|=\left|\sum _{{k=n+1}}^{\infty }w^{k}s(2^{k}x)\right|=\left|w^{{n+1}}\sum _{{k=0}}^{\infty }w^{k}s(2^{{k+n+1}}x)\right|\leq {\frac {|w|^{{n+1}}}{2}}\cdot {\frac {1}{1-|w|}}$ for all x when $|w|<1$ .

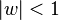This value can be made as small as we want by selecting a big enough value of n. Therefore, by the uniform limit theorem, $T_{w}$ is continuous if |w|<1.

The special case of the parabola

For $w=1/4$ , one obtains the parabola: the construction of the parabola by midpoint subdivision was described by Archimedes.

Differentiability

The Takagi curve is a fractal for parameters $w\neq 1/4$ , as it is nowhere differentiable.

Graphical construction

The blancmange curve can be visually built up out of triangle wave functions if the infinite sum is approximated by finite sums of the first few terms. In the illustration below, progressively finer triangle functions (shown in red) are added to the curve at each stage.


n = 0	n ≤ 1	n ≤ 2	n ≤ 3

Recursive Definition

The periodic version of the Takagi curve can also be defined recursively by:

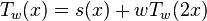$T_{w}(x)=s(x)+wT_{w}(2x)$ .

The version restricted to the unit interval can also be defined recursively by:

$T_{w}(x)={\begin{cases}x+wT_{w}(2x)&{\text{if }}0\leq x\leq 1/2\\(1-x)+wT_{w}(2x-1)&{\text{if }}1/2<x\leq 1.\end{cases}}$

Proof:

${\begin{aligned}T_{w}(x)&=\sum _{{n=0}}^{\infty }w^{n}s(2^{{n}}x)\\&=s(x)+\sum _{{n=1}}^{\infty }w^{n}s(2^{{n}}x)\\&=s(x)+w\sum _{{n=0}}^{\infty }w^{n}s(2^{{n+1}}x)\\&=s(x)+wT_{w}(2x)\end{aligned}}$ .

Other Properties

Integrating the Blancmange curve

Given that the integral of 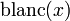${{\rm {blanc}}}(x)$ from 0 to 1 is 1/2, the identity ${{\rm {blanc}}}(x)={{\rm {blanc}}}(2x)/2+s(x)$ allows the integral over any interval to be computed by the following relation. The computation is recursive with computing time on the order of log of the accuracy required.

${\begin{aligned}I(x)&=\int _{0}^{x}{{\rm {blanc}}}(x)\,dx,\\I(x)&={\begin{cases}1/2+I(x-1)&{\text{if }}x\geq 1\\1/2-I(1-x)&{\text{if }}1/2<x<1\\I(2x)/4+x^{2}/2&{\text{if }}0\leq x\leq 1/2\\-I(-x)&{\text{if }}x<0\end{cases}}\\\int _{a}^{b}{{\rm {blanc}}}(x)\,dx&=I(b)-I(a).\end{aligned}}$

Relation to simplicial complexes

Let

$N={\binom {n_{t}}{t}}+{\binom {n_{{t-1}}}{t-1}}+\ldots +{\binom {n_{j}}{j}},\quad n_{t}>n_{{t-1}}>\ldots >n_{j}\geq j\geq 1.$

Define the Kruskal–Katona function

$\kappa _{t}(N)={n_{t} \choose t+1}+{n_{{t-1}} \choose t}+\dots +{n_{j} \choose j+1}.$

The Kruskal–Katona theorem states that this is the minimum number of (t − 1)-simplexes that are faces of a set of N t-simplexes.

As t and N approach infinity, 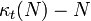$\kappa _{t}(N)-N$ (suitably normalized) approaches the blancmange curve.

References

Weisstein, Eric W., "Blancmange Function", MathWorld.
Teiji Takagi, "A Simple Example of a Continuous Function without Derivative", Proc. Phys. Math. Japan, (1903) Vol. 1, pp. 176–177.
Benoit Mandelbrot, "Fractal Landscapes without creases and with rivers", appearing in The Science of Fractal Images, ed. Heinz-Otto Peitgen, Dietmar Saupe; Springer-Verlag (1988) pp 243–260.
Linas Vepstas, Symmetries of Period-Doubling Maps, (2004)
Donald Knuth, The Art of Computer Programming, volume 4a. Combinatorial algorithms, part 1. ISBN 0-201-03804-8. See pages 372-375.

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.