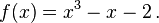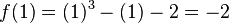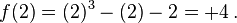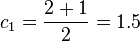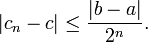Bisection method
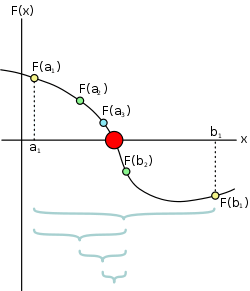
The bisection method in mathematics is a root-finding method that repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow. Because of this, it is often used to obtain a rough approximation to a solution which is then used as a starting point for more rapidly converging methods.[1] The method is also called the interval halving method,[2] the binary search method,[3] or the dichotomy method.[4]
The method
The method is applicable when we wish to solve the equation f(x) = 0 for the real variable x, where f is a continuous function defined on an interval [a, b] and f(a) and f(b) have opposite signs. In this case a and b are said to bracket a root since, by the intermediate value theorem, the f must have at least one root in the interval (a, b).
At each step the method divides the interval in two by computing the midpoint c = (a+b) / 2 of the interval and the value of the function f(c) at that point. Unless c is itself a root (which is very unlikely, but possible) there are now two possibilities: either f(a) and f(c) have opposite signs and bracket a root, or f(c) and f(b) have opposite signs and bracket a root. The method selects the subinterval that is a bracket as a new interval to be used in the next step. In this way the interval that contains a zero of f is reduced in width by 50% at each step. The process is continued until the interval is sufficiently small.
Explicitly, if f(a) and f(c) are opposite signs, then the method sets c as the new value for b, and if f(b) and f(c) are opposite signs then the method sets c as the new a. (If f(c)=0 then c may be taken as the solution and the process stops.) In both cases, the new f(a) and f(b) have opposite signs, so the method is applicable to this smaller interval.[5]
Example: Finding the root of a polynomial
Suppose that the bisection method is used to find a root of the polynomial
First, two numbers  and
and  have to be found such that
have to be found such that 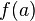 and
and 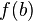 have opposite signs. For the above function,
have opposite signs. For the above function,  and
and 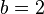 satisfy this criterion, as
satisfy this criterion, as
and
Because the function is continuous, there must be a root within the interval [1, 2].
In the first iteration, the end points of the interval which brackets the root are 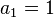 and
and 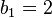 , so the midpoint is
, so the midpoint is
The function value at the midpoint is 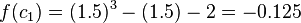 . Because
. Because  is negative,
is negative,  is replaced with
is replaced with 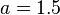 for the next iteration to ensure that
for the next iteration to ensure that 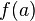 and
and 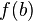 have opposite signs. As this continues, the interval between
have opposite signs. As this continues, the interval between  and
and  will become increasingly smaller, converging on the root of the function. See this happen in the table below.
will become increasingly smaller, converging on the root of the function. See this happen in the table below.
| Iteration |  | 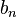 |  | 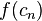 |
|---|---|---|---|---|
| 1 | 1 | 2 | 1.5 | −0.125 |
| 2 | 1.5 | 2 | 1.75 | 1.6093750 |
| 3 | 1.5 | 1.75 | 1.625 | 0.6660156 |
| 4 | 1.5 | 1.625 | 1.5625 | 0.2521973 |
| 5 | 1.5 | 1.5625 | 1.5312500 | 0.0591125 |
| 6 | 1.5 | 1.5312500 | 1.5156250 | −0.0340538 |
| 7 | 1.5156250 | 1.5312500 | 1.5234375 | 0.0122504 |
| 8 | 1.5156250 | 1.5234375 | 1.5195313 | −0.0109712 |
| 9 | 1.5195313 | 1.5234375 | 1.5214844 | 0.0006222 |
| 10 | 1.5195313 | 1.5214844 | 1.5205078 | −0.0051789 |
| 11 | 1.5205078 | 1.5214844 | 1.5209961 | −0.0022794 |
| 12 | 1.5209961 | 1.5214844 | 1.5212402 | −0.0008289 |
| 13 | 1.5212402 | 1.5214844 | 1.5213623 | −0.0001034 |
| 14 | 1.5213623 | 1.5214844 | 1.5214233 | 0.0002594 |
| 15 | 1.5213623 | 1.5214233 | 1.5213928 | 0.0000780 |
After 13 iterations, it becomes apparent that there is a convergence to about 1.521: a root for the polynomial.
Analysis
The method is guaranteed to converge to a root of f if f is a continuous function on the interval [a, b] and f(a) and f(b) have opposite signs. The absolute error is halved at each step so the method converges linearly, which is comparatively slow.
Specifically, if c1 = (a+b)/2 is the midpoint of the initial interval, and cn is the midpoint of the interval in the nth step, then the difference between cn and a solution c is bounded by[6]
This formula can be used to determine in advance the number of iterations that the bisection method would need to converge to a root to within a certain tolerance.
The number of iterations needed, n, to achieve a given error (or tolerance), ε, is given by:
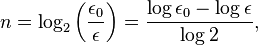
where 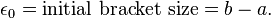
Therefore, the linear convergence is expressed by 
Pseudocode
The method may be written in Pseudocode as follows:[7]
INPUT: Function f, endpoint values a, b, tolerance TOL, maximum iterations NMAX CONDITIONS: a < b, either f(a) < 0 and f(b) > 0 or f(a) > 0 and f(b) < 0 OUTPUT: value which differs from a root of f(x)=0 by less than TOL
N ← 1
While N ≤ NMAX # limit iterations to prevent infinite loop
c ← (a + b)/2 # new midpoint
If f(c) = 0 or (b – a)/2 < TOL then # solution found
Output(c)
Stop
EndIf
N ← N + 1 # increment step counter
If sign(f(c)) = sign(f(a)) then a ← c else b ← c # new interval
EndWhile
Output("Method failed.") # max number of steps exceeded
See also
- Secant method
- Newton's method
- Root-finding algorithm
- Binary search algorithm
- Lehmer–Schur algorithm, generalization of the bisection method in the complex plane
- Nested intervals
- Brent's method
References
- ↑ Burden & Faires 1985, p. 31
- ↑ http://siber.cankaya.edu.tr/NumericalComputations/ceng375/node32.html
- ↑ Burden & Fairies 1985, p. 28
- ↑ Encyclopedia of Mathematics
- ↑ Burden & Faires 1985, p. 28 for section
- ↑ Burden & Faires 1985, p. 31, Theorem 2.1
- ↑ Burden & Faires 1985, p. 29
- Burden, Richard L.; Faires, J. Douglas (1985), "2.1 The Bisection Algorithm", Numerical Analysis (3rd ed.), PWS Publishers, ISBN 0-87150-857-5.
- Corliss, George (1977), "Which root does the bisection algorithm find?", SIAM Review 19 (2): 325–327, doi:10.1137/1019044, ISSN 1095-7200.
- Kaw, Autar; Kalu, Egwu (2008), Numerical Methods with Applications (1st ed.)
External links
| Wikiversity has learning materials about The bisection method |
| The Wikibook Numerical Methods has a page on the topic of: Equation Solving |
- Weisstein, Eric W., "Bisection", MathWorld.
- Bisection Method Notes, PPT, Mathcad, Maple, Matlab, Mathematica from Holistic Numerical Methods Institute
- Module for the Bisection Method by John H. Mathews
- Online root finding of a polynomial-Bisection method by Farhad Mazlumi