Biregular graph
| Graph families defined by their automorphisms | ||||
| distance-transitive |  | distance-regular |  | strongly regular |
 | ||||
| symmetric (arc-transitive) |  | t-transitive, t ≥ 2 | ||
 (if connected) (if connected) | ||||
| vertex- and edge-transitive |  | edge-transitive and regular |  | edge-transitive |
 |  |  | ||
| vertex-transitive |  | regular |  | (if bipartite) biregular |
 | ||||
| Cayley graph | skew-symmetric | asymmetric | ||
In graph-theoretic mathematics, a biregular graph[1] or semiregular bipartite graph[2] is a bipartite graph 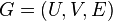 for which every two vertices on the same side of the given bipartition have the same degree as each other. If the degree of the vertices in
for which every two vertices on the same side of the given bipartition have the same degree as each other. If the degree of the vertices in  is
is  and the degree of the vertices in
and the degree of the vertices in  is
is  , then the graph is said to be
, then the graph is said to be  -biregular.
-biregular.
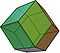
Example
Every complete bipartite graph  is
is  -biregular.[3]
The rhombic dodecahedron is another example; it is (3,4)-biregular.[4]
-biregular.[3]
The rhombic dodecahedron is another example; it is (3,4)-biregular.[4]
Vertex counts
An  -biregular graph
-biregular graph 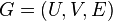 must satisfy the equation
must satisfy the equation  . This follows from a simple double counting argument: the number of endpoints of edges in
. This follows from a simple double counting argument: the number of endpoints of edges in  is
is 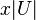 , the number of endpoints of edges in
, the number of endpoints of edges in  is
is 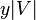 , and each edge contributes the same amount (one) to both numbers.
, and each edge contributes the same amount (one) to both numbers.
Symmetry
Every regular bipartite graph is also biregular. Every edge-transitive graph (disallowing graphs with isolated vertices) that is not also vertex-transitive must be biregular.[3] In particular every edge-transitive graph is either regular or biregular.
Configurations
The Levi graphs of geometric configurations are biregular; a biregular graph is the Levi graph of an (abstract) configuration if and only if its girth is at least six.[5]
References
- ↑ Scheinerman, Edward R.; Ullman, Daniel H. (1997), Fractional graph theory, Wiley-Interscience Series in Discrete Mathematics and Optimization, New York: John Wiley & Sons Inc., p. 137, ISBN 0-471-17864-0, MR 1481157.
- ↑ Dehmer, Matthias; Emmert-Streib, Frank (2009), Analysis of Complex Networks: From Biology to Linguistics, John Wiley & Sons, p. 149, ISBN 9783527627998.
- ↑ 3.0 3.1 Lauri, Josef; Scapellato, Raffaele (2003), Topics in Graph Automorphisms and Reconstruction, London Mathematical Society Student Texts, Cambridge University Press, pp. 20–21, ISBN 9780521529037.
- ↑ Réti, Tamás (2012), "On the relationships between the first and second Zagreb indices", MATCH Commun. Math. Comput. Chem. 68: 169–188.
- ↑ Gropp, Harald (2007), "VI.7 Configurations", in Colbourn, Charles J.; Dinitz, Jeffrey H., Handbook of combinatorial designs, Discrete Mathematics and its Applications (Boca Raton) (Second ed.), Chapman & Hall/CRC, Boca Raton, FL, pp. 353–355.