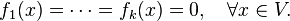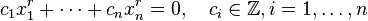Birch's theorem

From Wikipedia, the free encyclopedia

In mathematics, Birch's theorem,^[1] named for Bryan John Birch, is a statement about the representability of zero by odd degree forms.

Statement of Birch's theorem

Let K be an algebraic number field, k, l and n be natural numbers, r₁, . . . ,r_k be odd natural numbers, and f₁, . . . ,f_k be homogeneous polynomials with coefficients in K of degrees r₁, . . . ,r_k respectively in n variables, then there exists a number ψ(r₁, . . . ,r_k,l,K) such that

$n\geq \psi (r_{1},\ldots ,r_{k},l,K)$

implies that there exists an l-dimensional vector subspace V of Kⁿ such that

$f_{1}(x)=\cdots =f_{k}(x)=0,\quad \forall x\in V.$

Remarks

The proof of the theorem is by induction over the maximal degree of the forms f₁, . . . ,f_k. Essential to the proof is a special case, which can be proved by an application of the Hardy–Littlewood circle method, of the theorem which states that if n is sufficiently large and r is odd, then the equation

$c_{1}x_{1}^{r}+\cdots +c_{n}x_{n}^{r}=0,\quad c_{i}\in {\mathbb {Z}},i=1,\ldots ,n$

has a solution in integers x₁, . . . ,x_n, not all of which are 0.

The restriction to odd r is necessary, since even-degree forms, such as positive definite quadratic forms, may take the value 0 only at the origin.

References

↑ B. J. Birch, Homogeneous forms of odd degree in a large number of variables, Mathematika, 4, pages 102–105 (1957)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.