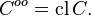Bipolar theorem
From Wikipedia, the free encyclopedia
In mathematics, the bipolar theorem is a theorem in convex analysis which provides necessary and sufficient conditions for a cone to be equal to its bipolar. The bipolar theorem can be seen as a special case of the Fenchel–Moreau theorem.[1]:76–77
Statement of theorem
For any nonempty set  in some linear space
in some linear space  , then the bipolar cone
, then the bipolar cone 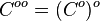 is given by
is given by
where  denotes the convex hull.[1]:54[2]
denotes the convex hull.[1]:54[2]
Special case
 is a nonempty closed convex cone if and only if
is a nonempty closed convex cone if and only if  when
when 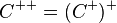 , where
, where 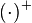 denotes the positive dual cone.[2][3]
denotes the positive dual cone.[2][3]
Or more generally, if  is a convex cone then the bipolar cone is given by
is a convex cone then the bipolar cone is given by
Relation to Fenchel–Moreau theorem
If  is the indicator function for a cone
is the indicator function for a cone  . Then the convex conjugate
. Then the convex conjugate  is the support function for
is the support function for  , and
, and  . Therefore
. Therefore  if and only if
if and only if  .[1]:54[3]
.[1]:54[3]
References
- ↑ 1.0 1.1 1.2 Borwein, Jonathan; Lewis, Adrian (2006). Convex Analysis and Nonlinear Optimization: Theory and Examples (2 ed.). Springer. ISBN 9780387295701.
- ↑ 2.0 2.1 Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. pp. 51–53. ISBN 9780521833783. Retrieved October 15, 2011.
- ↑ 3.0 3.1 Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. pp. 121–125. ISBN 9780691015866.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.