Bipartite matroid

From Wikipedia, the free encyclopedia

In mathematics, a bipartite matroid is a matroid all of whose circuits have even size.

Example

A uniform matroid 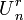$U{}_{n}^{r}$ is bipartite if and only if $r$ is an odd number, because the circuits in such a matroid have size 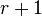$r+1$ .

Relation to bipartite graphs

Eulerian matroids were defined by Welsh (1969) as a generalization of the bipartite graphs, graphs in which every cycle has even size. A graphic matroid is bipartite if and only if it comes from a bipartite graph.^[1]

Duality with Eulerian matroids

An Eulerian graph is one in which all vertices have even degree; Eulerian graphs may be disconnected. For planar graphs, the properties of being bipartite and Eulerian are dual: a planar graph is bipartite if and only if its dual graph is Eulerian. As Welsh showed, this duality extends to binary matroids: a binary matroid is bipartite if and only if its dual matroid is an Eulerian matroid, a matroid that can be partitioned into disjoint circuits.

For matroids that are not binary, the duality between Eulerian and bipartite matroids may break down. For instance, the uniform matroid 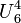$U{}_{6}^{4}$ is non-bipartite but its dual 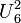$U{}_{6}^{2}$ is Eulerian, as it can be partitioned into two 3-cycles. The self-dual uniform matroid $U{}_{6}^{3}$ is bipartite but not Eulerian.

Computational complexity

It is possible to test in polynomial time whether a given binary matroid is bipartite.^[2] However, any algorithm that tests whether a given matroid is Eulerian, given access to the matroid via an independence oracle, must perform an exponential number of oracle queries, and therefore cannot take polynomial time.^[3]

References

↑ Welsh, D. J. A. (1969), "Euler and bipartite matroids", Journal of Combinatorial Theory 6: 375–377, MR 0237368 .
↑ Lovász, László; Seress, Ákos (1993), "The cocycle lattice of binary matroids", European Journal of Combinatorics 14 (3): 241–250, doi:10.1006/eujc.1993.1027, MR 1215334 .
↑ Jensen, Per M.; Korte, Bernhard (1982), "Complexity of matroid property algorithms", SIAM Journal on Computing 11 (1): 184–190, doi:10.1137/0211014, MR 646772 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.