Biorthogonal system

From Wikipedia, the free encyclopedia

In mathematics, a biorthogonal system is a pair of indexed families of vectors

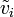${\tilde v}_{i}$ in

E

and ${\tilde u}_{i}$ in

F

such that

$\langle {\tilde v}_{i},{\tilde u}_{j}\rangle =\delta _{{i,j}},$

where E and F form a pair of topological vector spaces that are in duality, $⟨, ⟩$ is a bilinear mapping and 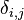$\delta _{{i,j}}$ is the Kronecker delta.

A biorthogonal system in which $<var>E</var> = <var>F</var>$ and 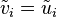${\tilde v}_{i}={\tilde u}_{i}$ is an orthonormal system.

An example is the pair of sets of respectively left and right eigenvectors of a matrix, indexed by eigenvalue.^{[citation needed]}

Projection

Related to a biorthogonal system is the projection

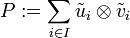$P:=\sum _{{i\in I}}{\tilde u}_{i}\otimes {\tilde v}_{i}$ ,

where 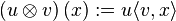$\left(u\otimes v\right)(x):=u\langle v,x\rangle$ ; its image is the linear span of $\{{\tilde u}_{i}:i\in I\}$ , and the kernel is $\{\langle {\tilde v}_{i},\cdot \rangle =0:i\in I\}$ .

Construction

Given a possibly non-orthogonal set of vectors 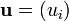${\mathbf {u}}=(u_{i})$ and ${\mathbf {v}}=(v_{i})$ the projection related is

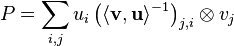$P=\sum _{{i,j}}u_{i}\left(\langle {\mathbf {v}},{\mathbf {u}}\rangle ^{{-1}}\right)_{{j,i}}\otimes v_{j}$ ,

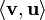where $\langle {\mathbf {v}},{\mathbf {u}}\rangle$ is the matrix with entries $\left(\langle {\mathbf {v}},{\mathbf {u}}\rangle \right)_{{i,j}}=\langle v_{i},u_{j}\rangle$ .

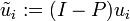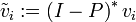${\tilde u}_{i}:=(I-P)u_{i}$ , and ${\tilde v}_{i}:=\left(I-P\right)^{*}v_{i}$ then is an orthogonal system.

References

Jean Dieudonné, On biorthogonal systems Michigan Math. J. 2 (1953), no. 1, 7–20

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Biorthogonal system

Projection

Construction

See also

References